AI 부트캠프 5주 : Linear Models
코드스테이츠와 함께하는 ‘AI 부프캠프’ 5주차
전반적 회고🎈
코드스테이츠 AI부트캠프 Section2 Sprint1에서 Linear Models을 학습하였다. Section2에서 본격적으로 Machine learning을 배운다고하여 기대 반, 걱정 반으로 시작하였다. 선형모델과 각종 평가지표를 공부하며 하나씩 답을 얻어가는 느낌으로, 어두움을 밝히는 느낌이 들었다.
각종 평가지표를 공부하며 분석 목적과 방향에 따라서 평가가 달라질 수 있으며, 상황에 따라서 적절한 평가지표를 사용해야 함을 알았다. 내가 왜 데이터분석을 하고자 하는지를 먼저 알아야 적절한 평가를 할 수 있는 것이다. 나는 왜 데이터분석을 하는걸까?
다양한 토이데이터를 통해서 적절한 분석과 평가를 하는 연습을 해야겠다.
학습 내용📚
N211 : Linear Regression
- 머신러닝
- 머신러닝이란 데이터로부터 유용한 예측을 하기 위해 모델이라고 불리는 소프트웨어를 학습시키는 과정을 말함
- 머신러닝 모델이란 예측에 활용할 수 있는 데이터 간의 수학적 관계, 규칙, 패턴 등을 의미
- 머신러닝의 목적은 기존의 데이터로부터 패턴을 학습한 뒤 새로운 데이터가 들어왔을 때 예측을 잘 하는 것
- 지도학습
- 지도 학습이란 주어진 데이터 가운데 Feature를 통하여 Target을 Inference하기 위한 Model을 만들고, Evaluation을 통하여 최적화하는 과정
- 기준모델
- 가장 간단하면서도 직관적이며 최소한의 성능을 나타내는 기준이 되는 모델
- 회귀문제: 타겟의 평균값 (평균 기준모델)
- 분류문제: 타겟의 최빈 클래스 (최빈값 기준모델)
- 시계열회귀문제: 이전 타임스탬프의 값
- 선형회귀모델
- 예측값과 실제값의 차이가 최소가 되게하는 것
- 선형회귀모델 평가지표에는 MSE, RMSE, MAE, R-squared 있음
- 산점도(scatterplot)에 가장 잘 맞는(best fit) 직선을 그려주면 그것이 회귀 예측모델
- 모델의 예측값과 실제값의 차이, 곧 잔차(residual)를 최소로 하는 선
- 실제값 : $ y $
- 단순선형회귀모델(예측값) : ${\hat y} = \hat{\alpha}x + \hat{\beta} $
- 잔차 : $ y - (\hat{\alpha}x + \hat{\beta}) $
cf) 오차(error)는 모집단에서의 예측값과 실제값의 차이. 하지만 통상적으로는 같은 의미로 사용
- 단순선형회귀 파이썬 함수구현
def reg_simple(x_arr, y_arr): """ 단순선형회귀 회귀계수와 상구항 구하기 """ x_m = sum(x_arr) / len(x_arr) y_m = sum(y_arr) / len(y_arr) x_diff_s = 0 xy_diff = 0 for i in range(len(x_arr)): x_diff_s += (x_arr[i] - x_m)**2 xy_diff += (x_arr[i] - x_m) * (y_arr[i] - y_m) reg_simple_a = xy_diff / x_diff_s reg_simple_b = y_m - (reg_simple_a * x_m) return (reg_simple_a, reg_simple_b)
외삽을 했을 때의 문제점은 무엇이 있을까요?
데이터에 없는 값을 예측하기 때문에 보다 도전적이고, 창의적일 수 있고, 가능성을 예측하는 것에는 좋을 수 있을 것 같다.
하지만 예측값이 맞는지 확인하기 힘들기 때문에 정말 순수한 추정이 될 수밖에 없다.
또한 “기술적 특이점이 나타날 경우 특이점 이후의 일은 외삽법으론 예측이 불가능”하다고 한다. 여기서 ‘기술적 특이점’이란 수학적으로는 미분계수가 0이 되는 변곡점을 의미한다. 곧 직선이 아닌 곡선으로 추정하는 경우 외삽은 전혀 다른 값을 예측하게 될 것으로 보인다.
머신러닝은 왜 새로운 프로그래밍 패러다임인가요?
기존의 프로그래밍은 데이터에 사용자가 규칙과 패턴을 입력하면 답을 주었지만, 머신러닝은 데이터와 답을 가지고 컴퓨터가 규칙과 패턴을 찾아낸다.
이때 기존 프로그래밍에서 사용자가 입력하는 규칙과 패턴은 사용자의 능력, 통찰력, 곧 인간적인 요소에 달려있다. 그렇기 때문에 규칙과 패턴은 ‘인간적’인 것이다.
하지만 머신러닝은 데이터와 답을 가지고 컴퓨터가 규칙과 패턴을 찾기 때문에 더욱 ‘객관적’인 규칙과 패턴이라 할 수 있다.
기준모델은 무엇이며 왜 필요한가요?
가장 간단하면서도 직관적이며 최소한의 성능을 나타내는 기준이 되는 모델
컴퓨터가 머신러닝을 통하여 만들어낸 모델이 얼마나 적합한지 비교하기 위하여 만든 모델이 기준모델
회귀 평가지표에는 어떤 것이 있으며 각각의 특징은 무엇인가요?
잔차제곱평균(MSE), 잔차제곱평균의 제곱근(RMSE), 잔차절대값평균(MAE), 결정계수($R^2$)
- MSE (Mean Squared Error)
- 잔차의 합이 0이 되는 것을 방지하기 위하여 잔차를 제곱
- 제곱을 하기 때문에 이상치에 영향을 크게 받음
- 모든 함수 값에서 미분가능 → 경사하강법을 통해 잔차가 최소화되는 지점을 찾을 수 있음
- 잔차의 절대값이 0~1이면 잔차가 작아지고, 잔차의 절대값이 1보다 크면 잔차가 더 크게 반영됨
- RMSE (Root Mean Squared Error)
- RMSE은 이상치에 대한 민감도가 MSE와 MAE 사이
- 실제값과 비슷하기 때문에 MSE에 비해 이해하기 쉬움
- MSE는 부드러운 곡선형으로 오차 함수가 그려지지만, RMSE는 그 MSE에서 루트를 취하기 때문에 미분 불가능한 지점, 뾰족한 지점을 갖음
- ❓❓모든 오차에 동일한 가중치를 부여❓❓
- MAE (Mean absolute error)
- 직관적으로 이해하기 쉬움
- 이상치에 둔감 혹은 강건robust
- 뾰족한 지점이 있어서, 미분 불가능한 지점이 있음
- R-squared (Coefficient of determination)
- 독립변수가 종속변수를 얼마만큼 설명해주는지를 가리키는 지표
- 설명력
\(R^2 = \frac{SSE}{SST} = 1 - \frac{SSR}{SST}\)
- SSE = 예측모델과 기준모델(평균)의 차이
- SST = 실제값과 기준모델(평균)의 차이
- SSR = 실제값과 예측모델의 차이
- 어떤 평가지표를 사용해야 할까?
- 이상치의 영향을 가장 덜받고 싶으면 MAE
- 모든 지점에서 미분가능하여, 모든 지점에서 잔차의 최소값을 찾고 싶으면 MSE
- ❓❓모델 학습 시 이상치에 가중치를 부여하고자 한다면 RMSE를 채택❓❓
선형회귀모델은 어떻게 해석할 수 있나요?
- 회귀계수 : 해당 독립변수가 한 단위 증가할 때마다 종속변수의 변화량
- Y절편 : 모든 독립변수가 0일 때 종속변수의 예측값
다항선형회귀도 역시 선형회귀입니다. 왜일까요? 선형회귀에서 말하는 선형성이란 무엇일까요?

- 3차 다항회귀선 역시 선형이라 할 수 있음
-
통계적 추정, 함수는 비선형이지만, 회귀함수 $ E(y x) $가 데이터에서 추정되는 파라미터가 선형이라는 점에서 선형이라고 할 수 있음 -
The regression function $ E(y x) $ is linear in the unknown parameters that are estimated from the data.
-
-
이러한 이유로 다항회귀(polynomial regression) 역시 다중선형되귀의 특수한 경우로 여겨짐
- 참고 : Linear regression
- 참고 : Linearity
Feature를 많이 투입하는 것은?
- Feature를 많이 투입해서 설명력을 높이는 모델은 어떻까?
- 상관관계가 높은 Feature 7개 투입
- 에러 발생
ValueError: X has 7 features, but LinearRegression is expecting 3 features as input.
- 피처는 3개까지만 넣는 것으로…😅
- 에러 발생
상관관계가 낮은 Feature로 모델을 만들면?
- 상관관계가 낮은 ‘yr_renovated’, ‘sqft_lot’, ‘sqft_lot15’ 투입
- 결정계수(R^2)가 -3439673205.52, 음수로 나옴
- 구글링결과 “model이 그냥 mean value로 예측하는 모델보다 예측성능이 더 낮은 비정상적인 경우를 의미” 한다고 함
- 평균으로 만든 기준모델보다 떨어진다는 의미로 해석할 수 있을 듯😉
독립변수를 1차원 행렬(벡터)로 만들면?
- 단순회귀의 경우 독립변수를 다음과 같이 1차원 행렬로 만들면
feature = 'GrLivArea' target = 'SalePrice' X = df[feature] y = df[target] simple_ols = LinearRegression() simple_ols.fit(X, y) - 다음과 같은 에러를 얻게 됨
ValueError: Expected 2D array, got 1D array instead:
array=[1710 1262 1786 … 2340 1078 1256].
Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample. - 1D array 말고 2D array를 사용하라는 에러😮
- 다음과 같이 독립변수는 대괄호로 감싸서 2차원 행렬로 만들어야 작동함
feature = ['GrLivArea'] target = 'SalePrice' X = df[feature] y = df[target] simple_ols = LinearRegression() simple_ols.fit(X, y)
선형회귀를 위한 가정들은 무엇인가?
(1) 선형성
(2) 독립성
- 완벽한 다중공선성 없음(no perfect multicollinearity) : Qxx = E[ xi xiT ] is a positive-definite matrix;
(3) 등분산성
-
등분산(homoscedasticity) : Var[ εi xi ] = σ2. - 등분산성의 주체는 잔차(표준화 잔차)
(4) 정규성
- 독립적으로 관찰된 개별값(iid observations) : (xi, yi) is independent from, and has the same distribution as, (xj, yj) for all i ≠ j;
N212 : Generalization
머신러닝의 개념을 ‘데이터를 통하여 일반화를 위한 효과적인 방법으로 계산하기 위한 연구’라고 한다면, 일반화는 머신러닝의 심장과도 같은 것
- 일반화(Generalization)
- 모델을 만드는 데 사용된 분포와 동일한 분포에서 추출한 이전에는 볼 수 없었던 새로운 데이터에 적절하게 적응하는 모형의 능력
- 편향과 분산(Bias & Variance)
- 가로축 = 모델의 복잡성
- 모델의 복잡성이 증가하면 분산이 커짐
- 세로축 = 모델의 점수
- 모델의 복잡성이 감수하면 편향이 커짐
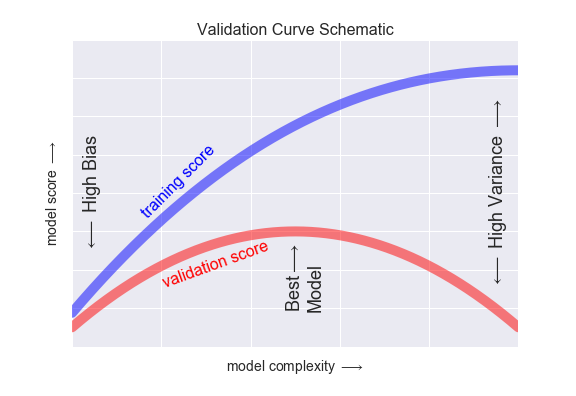
- 가로축 = 모델의 복잡성
-
과적합 (overfitting)
- 과적합은 훈련 데이터셋의 디테일과 노이즈까지 모두 학습하여 새로운 데이터를 잘 예측하지 못하는 현상
- 과적합 된 모델은 훈련 데이터셋에서의 성능은 높지만 테스트 데이터셋에서의 성능은 매우 낮음
- 과적합은 유연성이 높은 non-parametric모델이나 비선형 모델에서 나타날 가능성이 높음
- 선형회귀처럼 강력한 가정을 하지 않은 모델이기 때문에 유연하게 데이터를 학습하기 때문
- 과소적합 (underfitting)
- 과소적합은 훈련 데이터셋도 제대로 학습하지 못해서 새로운 데이터를 잘 예측하지 못하는 현상
- 과소적합 된 모델은 훈련 데이터셋에서의 성능과 테스트 데이터셋에서의 성능 모두 현저히 낮음
cross_val_score() 메써드에서 scoring 파라미터를 “neg_mean_absolute_error”와 같이 앞에 “neg_“를 붙이는데 이러한 이유는?
-
sklearn 에서 반환하는 MSE는 음수를 반환하기 때문에 “neg_” 를 붙여서 “저는 음수에요~”라고 말하는 것?
-
참조 : Metrics and scoring: quantifying the quality of predictions
test set는 training set와 다른 특징을 가진 데이터여서는 안 된다는데, 여기서 ‘다른 특징’이란 무엇이며, 구체적으로 특징을 비교하는 방법은 무엇인가?
- 데이터의 ‘분포’(분산, 왜도, 첨도 등)
- 강아지를 학습했는데, 호랑이로 평가한다면?
- 강아지와 호랑이는 ‘다른 특징’을 보임
모델을 평가하고 개선시킬 때는 어떤 방법을 사용할 수 있을까?
-
정규화(Regularization)/배깅(Bagging)/부스팅(Boosting)
- 정규화 regulaization
- 선형회귀 계수(Weight)에 대한 제약 조건을 추가함으로써 모형이 과도하게 구성되는 것을 방지해주는 방법
- 과최적화는 계수 크기를 과도하게 증가 하는 경향이 있기에, 정규화 방법에서의 제약조건은 일반적으로 계수의 크기를 제한함
- 정규화 방식은 릿지(Ridge) 와 라쏘(Lasso) 2가지 구분됨
- boosting
- 앙상블(Ensemble) 방식 중 하나로 부트스트래핑(Bootstraping)을 통해 여러 학습 데이터를 만들고 개별 모델을 통합하여 활용
- 배깅 기반의 대표 알고리즘으로 많이 사용하는 랜덤포레스트(Random Forest)가 있음
- bagging
- 앙상블(Ensemble) 방식 중 하나로 성능이 약한 학습기(week learner)를 여러 개 연결하여 강한 학습기(strong learner)로 만들어 감
- 앞에서 학습된 모델을 보완해나가면서 더 나은 모델로 학습시켜가는 방법
- 정규화 regulaization
일반화를 어떻게 정의할 수 있나요?
- 모델을 만드는 데 사용된 분포와 동일한 분포에서 추출한 이전에는 볼 수 없었던 새로운 데이터에 적절하게 적응하는 모형의 능력
데이터를 분리하는 이유는 무엇인가요?
- 학습과 평가를 위하여 = 일반화를 위하여
데이터 크기 별로 일반화 검증 방법이 어떻게 달라지나요?
- Performance estimation
- Large Dataset
- 2way holdout method
- confidence interval via normal approximation
- Small Dataset
- k-fold cross-validation without independent test set
- leave-one-out cross-validation without independent test set
- Confidence interval via 0.632(+) bootstrap
- Large Dataset
- Model selection(gyperparameter optimization) and performance estimation
- Large Dataset
- 3way holdout method
- Small Dataset
- k-fold cross-validation without independent test set
- leave-one-out cross-validation without independent test set
- Large Dataset
분산과 편향의 관계를 어떻게 정의할 수 있나요?
- 과적합은 큰 분산 적은 편향
- 과소적합은 작은 분산 큰 편향
- 분산과 편향은 트레이드오프관계
- 중간의 적절한 지점을 찾아야 함
과적합과 과소적합의 차이는 무엇인가요?
- 과소적합
- 훈련모델 점수, 평가모델 점수 모두 낮음
- 과대적합
- 훈련모델은 점수가 높지만, 평가모델은 점수가 낮음
cross_val_score() 함수의 파라미터 n_jobs 의 의미는?
- n_jobs : int, default=None
- Number of jobs to run in parallel. Training the estimator and computing the score are parallelized over the cross-validation splits. None means 1 unless in a joblib.parallel_backend context. -1 means using all processors. See Glossary for more details.
- 병렬실행 횟수
- 추정훈련과 점수계산은 교차검증 분할에 대하여 병렬화되어 수행됨
- joblib.parallel_backend 의 지시가 없는 한 None 은 1을 의미
- -1은 모든 프로세서 사용을 의미
- 자세한 내용은 용어집 참조
- 용어집 : n_jobs
- 이 파라미터는 동시사용 CPU 또는 스레드 수를 지정하는데 사용됨
- 1을 지정하면 병렬사용이 안됨
- 이는 디버깅에 유용
- -1로 설정하면 모든 CPU가 사용됨
- -1 미만으로 설정하면, 예를 들어 -2로 설정하면 하나를 제외한 모든 CPU를 사용함
N213 : Regularized Regression
정규화 회귀모델(Regularized Regression)
- 과적합을 방지하기 위한 방법
- 모델의 복잡도를 줄이는 방법
- 비용함수(RSS)에 ‘규제항’을 더해, 회귀계수 값에 제약을 가함
Ridge 회귀모형
- 규제항
- 가중치의 제곱합(squared sum of weights)
- L2 Penalty
- 영향력이 크지 않은 회귀계수의 값은 0에 가까운 수로 축소
Lasso 회귀모형
- Lasso(Least Absolute Shrinkage and Selection Operator)
- 규제항
- 가중치의 절대값의 합
- L1 Penalty
- 영향력이 크지 않은 회귀계수의 값을 0으로
- 영향력이 작은 특성은 제외하고, 큰 특성을 선택하는 효과
- 희소모델(sparse model)로 만드는 결과
Elastic Net 회귀모형
- 규제항
- 가중치의 절대값의 합과 제곱합을 동시
- L1 Penalty + L2 Penalty
λ (Lambda)
- lambda, alpha, penalty term, regularization term 등
- 패널티의 강도를 조절하는 하이퍼파라미터
- λ 의 크기가 클수록 회귀계수의 값이 줄어 듦
- $\lambda = 0$ 인 경우 기존의 선형회귀와 같아집니다.
- $\lambda = \infty $ 인 경우 $\beta = 0$ 이 됩니다.
과적합을 해소하기 위한 방법으로 무엇이 있나요?
- 모델의 복잡도를 줄이는 방법
- 차수(degree) 줄이기
- 특성 수 줄이기
- 더 많은 데이터를 학습
- 정규화
정규화(Regularization)란 무엇인가요?
- 선형모델에 규제항을 더해 과적합을 방지
- 규제항은 비용함수를 증가시켜 회귀계수를 감소
Ridge Regression과 Lasso Regression의 차이는 무엇인가요?
- Ridge : L2 Penalty(가중치들의 제곱합)
- 영향력이 크지 않은 회귀계수의 값은 0에 가까운 수로 축소
- Lasso : L1 Penalty(가중치들의 절댓값 합)
- 영향력이 크지 않은 회귀계수의 값을 0으로 만듦
- 특성을 선택하는 효과
- 희소모델(sparse model)을 만듦
- ElasticNet : L1 Penalty(가중치들의 절댓값 합) + L2 Penalty(가중치들의 제곱합)
람다(알파, 패널티)란 무엇인가요?
- 패널티의 강도를 조절하는 하이퍼파라미터
scikit-learn에서 최적의 알파값은 어떻게 찾을 수 있나요?
- RidgeCV(), LassoCV(), ElasticNetCV() 메써드 활용
Regularization 정규화의 의미
- Regularization 이라는 영어단어는 정규화라는 의미 이외에 규칙화, 정형화 로도 해석될 수 있음
- 훈련셋에서 학습한 모델이 테스트셋에서 오차가 크게 변하지 않도록, 곧 어드 데이터에도 적응할 수 있도록 정규화 하는 것
N214 : Logistic Regression
로지스틱회귀
- 어떤 범주에 속할 확률을 구하는 방법
- 로지스틱(sigmoid) 함수
- 선형회귀에 로지스틱 함수를 씌우면 확률을 구할 수 있음
- $ \sigma(x) = \large\frac{1}{1 + e^{-x}}$
- 로지스틱 회귀모델은 0과 1 사이의 값을 출력
- 출력값이 0.5 이상일 경우는 Class1로 0.5 미만일 경우는 Class0으로 분류

- 로지스틱 회귀계수
- 회귀계수가 양수인 경우 1일 확률이 높아지고 회귀계수가 음수인 경우 1일 확률이 낮아짐
- 회귀계수의 절대값이 클수록 영향력이 큼
정확도(Accuracy)
\(Accuracy = \frac{올바르게~예측한~수} {전체~예측~수}\)
혼동행렬(Confusion Matrix)
- confusion matrix(혼동행렬, 오차행렬)
- 분류기가 예측한 결과와 실제 결과에 대한 레코드의 개수를 표시한 테이블
- 예측 오류 및 오류의 유형을 아래와 같이 테이블 상에서 확인할 수 있습니다.
- TP(True Positive) : 실제 Positive인 것을 Positive라고 정확하게 예측한 경우
- 심장병이 있는 샘플을 심장병이 있다고 예측한 경우
- FP(False Positive) : 실제로는 Negative인데 Positive라고 잘못 예측한 경우
- 심장병이 없는 샘플을 심장병이 있다고 예측한 경우
- FN(False Negative) : 실제로는 Positive인데 Negative라고 잘못 예측한 경우
- 심장병이 있는 샘플을 심장병이 없다고 예측한 경우
- TN(True Negative) : 실제 Negative인 것을 Negative라고 정확하게 예측한 경우
- 심장병이 없는 샘플을 심장병이 없다고 예측한 경우

-
정확도(Accuracy) \(\large \frac{TP + TN}{Total}\)
-
정밀도(Precision) \(\large \frac{TP}{TP + FP}\)
-
재현율(Recall, Sensitivity) \(\large \frac{TP}{TP + FN}\)
-
F1점수(F1 score) : 정밀도와 재현율의 조화평균 \(2\cdot\large\frac{precision\cdot recall}{precision + recall}\)
-
임계값 조정
- 임계값을 낮추면 Class1로 예측하는 수가 많아짐
- 재현율 증가, 정밀도 감소
- 임계값을 높이면 Class1로 예측하는 수가 적어짐
- 재현율 감소, 정밀도 증가
- 임계값을 낮추면 Class1로 예측하는 수가 많아짐
ROC score
- ROC Curve는 여러 임계값에 대해 TPR(True Positive Rate, recall)과 FPR(False Positive Rate)을 그래프로 보여줌
Recall(재현율) = Sensitivity(민감도) = ${\displaystyle \mathrm {TPR} ={\frac {\mathrm {TP} }{\mathrm {P} }}={\frac {\mathrm {TP} }{\mathrm {TP} +\mathrm {FN} }}=1-\mathrm {FNR} }$
Fall-out(위양성률) = ${\displaystyle \mathrm {FPR} ={\frac {\mathrm {FP} }{\mathrm {N} }}={\frac {\mathrm {FP} }{\mathrm {FP} +\mathrm {TN} }}=1-\mathrm {TNR(Specificity)} }$
- 재현율을 높이기 위해서는 Positive로 판단하는 임계값을 계속 낮추어 모두 Positive로 판단하게 만들면 됩니다. 하지만 이렇게 하면 동시에 Negative이지만 Positive로 판단하는 위양성률도 같이 높아집니다.
- 임계값이 1인 경우 TPR, FPR 모두 0이 됩니다.
- 임계값이 0인 경우 TPR, FPR 모두 1이 됩니다.
AUC score
- ROC 곡선 아래의 면적
회귀 문제는 어떤 타겟값을 예측하는 문제인가요?
- 타겟이 연속형 변수인 경우
분류 문제는 어떤 타겟값을 예측하는 문제인가요?
- 타겟이 범주형 변수인 경우
회귀 문제와 분류 문제는 어떤 차이점이 있었나요?
- 회귀는 연속형 타겟의 예측값을 찾을 때 사용
- 분류는 범주형 타겟의 해당범주에 속할 확률을 찾을 때 사용
타겟값, 기준모델, 평가지표 등에서 분류 문제는 회귀 문제와 무엇이 다른가요?
- 회귀
- 타겟 : 연속형 변수
- 기준모델 : 평균값
- 평가지표 : MSE, RMSE, MAE, R2
- 분류
- 타겟 : 범주형 변수
- 기준모델 : 최빈값
- 평가지표 : 정확도, 재현율, 정밀도, F1 Score, ROC Curve, AUC Score
Logistic Regression과 Linear Regression의 차이는 무엇인가요?
- Logistic Regression
- 최대우도법을 사용하여 타겟의 확률을 추정
- Linear Regression
- 최소제곱법을 사용하여 타겟의 값을 추정
재현율과 정밀도는 무엇이며 이 둘은 왜 트레이드오프 관계에 있나요?
- 재현율 : 실제 양성인 케이스 가운데, 양성이라고 예측한 비율
- 정밀도 : 양성이라고 예측한 케이스 가운데 실제 양성인 비율
- 한정된 데이터 안에서 임계값을 낮추면 양성예측은 늘어나지만 음성예측은 줄어들기 때문에
AUC Score가 의미하는 것은 무엇인가요?
상황에 따른 평가지표 선택문제
- 심장병을 예측하는 경우
- 심장병인 사람을 심장병이 아니라고 예측하는 것(2종오류, FN)
- 심장병이 아닌 사람을 심장병이라고 예측하는 것(1종오류, FP)
- 이 경우 2종오류가 더 치명적
- FN이 고려되는 재현율(Recall)이 적절
- 넷플릭스에서 영화추천을 해주는 경우
- 좋아하는 영화를 좋아하지 않다고 예측(2종오류, FN)
- 좋아하지 않는 영화를 좋아한다고 예측(1종오류, FP)
- 이 경우 2종오류가 더 치명적
- FN이 고려되는 재현율(Recall)이 적절
- 스팸 메일을 분류하는 경우
- 스팸인데 스팸이 아니라고 예측(2종오류, FN)
- 스팸이 아닌데 스팸이라고 예측(1종오류, FP)
- 이 경우 1종오류가 더 치명적
- FP가 고려되는 정밀도(Precision)가 적절
- 자율주행 자동차가 사물을 인식하는 경우
- 사물인데 사물이 아니라고 인식(2종오류, FN)
- 사물이 아닌데 사물이라고 인식(1종오류, FP)
- 이경우 2종오류가 더 치명적
- FN이 고려되는 재현율(Recall)이 적절
요리도구 🔪
sklearn.linear_model.LogisticRegression()
- 사용법
sklearn.linear_model.LogisticRegression(penalty=’l2’, *, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’lbfgs’, max_iter=100, multi_class=’auto’, verbose=0, warm_start=False, n_jobs=None, l1_ratio=None)
파라미터
- penalty : {‘l1’, ‘l2’, ‘elasticnet’, None}, default=’l2’
- 패널티 놈의 종류
- 주의! 일부 패널티는 일부 solver에 작동하지 않음
- solver 파라미터에 따른 적절한 penalty 파라미터를 지정해야 함
- dual : bool, default=False
- dual, primal 식(formulation)
- 이중식은 l2 패널티와 liblinear 솔버에서만 실행됨
- 샘플 수 > 피쳐 수 이면 dual=False 로 하는데 적절함
- tol : float, default=1e-4
- 중지 기준의 오차 범위
- C : float, default=1.0
- 정규화강도의 역
- 양수(float)여야 함
- 작으면 강한 정규화
- fit_intercept : bool, default=True
- 결정함수(decision function)에 상수(bias, intercept)를 추가할지
- intercept_scaling : float, default=1
- 솔버가 ‘liblinear’, ‘self.fit_intercept’가 ‘True’로 설정된 경우에만 유용함 ❓❓❓
- 즉, x 가 [x, self.intercept_scaling] 가 됨
- 예를 들면, intercept_scaling 와 같은 상수 값을 가진 “synthetic” 피쳐가 인스턴스 벡터에 추가됨
- 이때 절편은 intercept_scaling synthetic_feature_weigh 가 됨 ❓❓❓
- synthetic feature weight 에 대한 정규화의 영향을 줄이려면 intercept_scaling을 늘려야 함
- class_weight : dict or ‘balanced’, default=None
- {class_label: weight} 형태의 클래스관련 가중치
- 지정되지 않으면 모든 클래스에 1의 가중치가 주어짐
- “balanced” 모드에서는 y값을 사용하여 입력데이터의 class frequencies 에 반비례하는 가중치를 “n_samples / (n_classes * np.bincount(y))”으로 자동 조절함
- sample_weight 가 지정된 경우 곱해짐
- random_state : int, RandomState instance, default=None
- solver == ‘sag’, ‘saga’ or ‘liblinear’ 인 경우 데이터를 셔플하는데 사용됨
- solver : {‘lbfgs’, ‘liblinear’, ‘newton-cg’, ‘newton-cholesky’, ‘sag’, ‘saga’}, default=’lbfgs’
- 최적화문제(optimization problem)에 사용되는 알고리즘
- solver 선택 기준
- 작은 데이터 세트의 경우 ‘liblinear’가 좋은 선택인 반면, 큰 데이터 세트의 경우 ‘sag’와 ‘saga’가 더 빠름
- 다중 클래스 문제의 경우 ‘newton-cg’, ‘sag’, ‘sag’ 및 ‘lbfgs’만이 다항식 손실을 처리할 수 있음
- ‘liblinear’ 은 ‘one-versus-rest’로 제한 됨
- 샘플 수가 피쳐 수보다 월등히 많은 경우 ‘newton-cholesky’가 적절함
- 특히 희귀한 범주(rare categories)를 가진 단일 핫 인코딩된 범주형 기능을 사용
- 이는 이진분류와 다중분류를 위한 ‘one-versus-rest’ 축소로 제한 됨
- 메모리 사용이 피쳐수 제곱에 영향을 받음(피쳐가 많은 경우 메모리 사용 많음)
- penalty 에 따른 solver 선택
- ‘lbfgs’ - [‘l2’, None]
- ‘liblinear’ - [‘l1’, ‘l2’]
- ‘newton-cg’ - [‘l2’, None]
- ‘newton-cholesky’ - [‘l2’, None]
- ‘sag’ - [‘l2’, None]
- ‘saga’ - [‘elasticnet’, ‘l1’, ‘l2’, None]
- max_iter : int, default=100
- 솔버가 수렴하는 데 사용되는 최대 반복 수
- multi_class : {‘auto’, ‘ovr’, ‘multinomial’}, default=’auto’
- ‘ovr’은 이항문제에 적합
- ‘multinomial’로 하는 경우 레이블이 이항이여도 전체 확률분포에 대하여 다항손실(multinomial loss)을 계산함
- solver=’liblinear’인 경우 ‘multinomial’ 사용 불가
- ‘auto’로 하면 데이터가 이항이거나 solver=’liblinear’인 경우에는 자동으로 ‘ovr’을 선택하고, 그렇지 않은경우에는 자동으로 ‘multinomial’을 선택
- verbose : int, default=0
- solver가 liblinear 와 lbfgs 인 경우 설명(verbosity)을 위해 양의정수를 높임
- warm_start : bool, default=False
- True로 설정되면 이전명령의 방법을 초기화에 맞추어 재사용하고, 그렇지 않으면 이전 방법을 삭제함
- solver가 liblinear인경우 사용 불가능
- n_jobs : int, default=None
- multi_class=’ovr’ 로 설정된 경우 병렬처리할 때 사용되는 CPU 코어 수
- solver가 ‘liblinear’로 설정된 경우 무시 됨
- joblib.parallel_backend 에서 따로 설정하지 않으면 None 은 기본적으로 1을 의미
- -1은 모든 프로세서 사용을 의미
- l1_ratio : float, default=None
- penalty=’elasticnet’ 인 경우 Elastic-Net 에서 l1의 범위 0 <= l1_ratio <= 1
- l1_ratio=0 으로 설정하는 경우 penalty=’l2’로 설정하는 것과 같음
- l1_ratio=1 으로 설정하는 경우 penalty=’l1’로 설정하는 것과 같음
- 0 < l1_ratio <1 으로 설정하는 경우 패널티는 l1과 l2의 조합
속성
- classes_ : ndarray of shape (n_classes, )
- 분류에 사용된 클레스 레이블의 목록
- coef_ : ndarray of shape (1, n_features) or (n_classes, n_features)
- 결정함수에서 특성들의 회귀계수
- coef_ 는 이항문제인 경우의 (1, n_features)의 형태임
- 다항의 경우 coef_는 1(True)에 해당하고, -coef_는 0(False)에 해당함
- intercept_ : ndarray of shape (1,) or (n_classes,)
- 결정함수(decision function)에 포함되는 절편(bias)
- fit_intercept 가 False로 설정되면 절편은 0
- intercept_ 는 이항문제일때는 (1,)의 형태이고, multi_class=’multinomial’로 되어 다항문제일 때는 intercept_는 1(True)에 해당하고, -intercept_는 0(False)에 해당함
- n_features_in_ : int
- fit에 사용된 특성(feature) 수
- feature_names_in_ : ndarray of shape (n_features_in_,)
- fit에 사용된 특성들의 이름
- 독립변수(X)에 사용된 모든 특성(feature)의 이름이 문자열인 경우에 사용
- n_iter_ : ndarray of shape (n_classes,) or (1, )
- 모든 클래스에 대한 실제 반복 횟수
- 이항 또는 다항의 경우 하나의 요소만 반환함
- solver가 ‘liblinear’ 인 경우 모든 클래스에서 최대 반복 횟수만 반환함
메써드
- decision_function(X)
- 표본의 신뢰 점수를 예측
- densify()
- 계수 행렬(coefficient matrix)을 밀도배열(dense array) 형식으로 변환
- fit(X, y[, sample_weight])
- 훈련데이터를 모델에 적합(투입, fit)
- get_params([deep])
- 해당 추정(estimator)에 사용된 파라미터를 반환
- predict(X)
- X 표본에 대한 y의 라벨을 예측
- predict_log_proba(X)
- 확률 추정치(probability estimates)의 로그값(logarithm)을 예측
- predict_proba(X)
- 확률 추정치
- score(X, y[, sample_weight])
- 주어진 데이터와 라벨에 대하여 평균 정확도(accuracy)를 반환
- set_params(**params)
- 해당 추정의 파라미터를 설정
- sparsify()
- 계수행렬(coefficient matrix)을 희소형식(sparse format)으로 변환
sklearn.linear_model.LogisticRegressionCV
- 교차검증(cross validation)이 내장(built-in) 된 Logistic regression
- 사용법
sklearn.linear_model.LogisticRegressionCV(*, Cs=10, fit_intercept=True, cv=None, dual=False, penalty=’l2’, scoring=None, solver=’lbfgs’, tol=0.0001, max_iter=100, class_weight=None, n_jobs=None, verbose=0, refit=True, intercept_scaling=1.0, multi_class=’auto’, random_state=None, l1_ratios=None)
파라미터
- Cs : int or list of floats, default=10
- Cs 값은 정규화강도(regularization strength)의 역을 표현
- Cs 값이 작으면 강한 정규화를 의미
- penalty : {‘l1’, ‘l2’, ‘elasticnet’}, default=’l2’
- ‘l2’: add a L2 penalty term (used by default);
- ‘l1’: add a L1 penalty term;
- ‘elasticnet’: both L1 and L2 penalty terms are added.
- solver : {‘lbfgs’, ‘liblinear’, ‘newton-cg’, ‘newton-cholesky’, ‘sag’, ‘saga’}, default=’lbfgs’
- 최적화에 사용되는 알고리즘
- ‘lbfgs’ - [‘l2’]
- ‘liblinear’ - [‘l1’, ‘l2’]
- ‘newton-cg’ - [‘l2’]
- ‘newton-cholesky’ - [‘l2’]
- ‘sag’ - [‘l2’]
- ‘saga’ - [‘elasticnet’, ‘l1’, ‘l2’]
sklearn.metrics.roc_auc_score
- Receiver Operating Characteristic Curve(ROC) 아래의 면적을 계산하여 점수(AUC Score)로 반환해주는 함수
- 이 메써드는 종속변수가 이항변수(Binary), 다항변수(Multi-class)인 경우에만 사용할 수 있음
사용법
- sklearn.metrics.roc_auc_score(y_true, y_score, *, average=’macro’, sample_weight=None, max_fpr=None, multi_class=’raise’, labels=None)
파라미터
- y_true : array-like of shape (n_samples,) or (n_samples, n_classes)
True labels or binary label indicators. The binary and multiclass cases expect labels with shape (n_samples,) while the multilabel case expects binary label indicators with shape (n_samples, n_classes). - y_score : array-like of shape (n_samples,) or (n_samples, n_classes)
Target scores.
반환
- auc : float
Area Under the Curve score.
sklearn.metrics.roc_curve
- Receiver Operating Characteristic(ROC) 를 계산
- 이 메써드는 종속변수가 이항변수(Binary)인 경우에만 사용할 수 있음
사용법
- sklearn.metrics.roc_curve(y_true, y_score, *, pos_label=None, sample_weight=None, drop_intermediate=True)
파라미터
- y_true : ndarray of shape (n_samples,)
True binary labels. If labels are not either {-1, 1} or {0, 1}, then pos_label should be explicitly given. - y_score : ndarray of shape (n_samples,)
Target scores, can either be probability estimates of the positive class, confidence values, or non-thresholded measure of decisions (as returned by “decision_function” on some classifiers).
반환
-
fpr : ndarray of shape (>2,)
Increasing false positive rates such that element i is the false positive rate of predictions with score >= thresholds[i]. -
tpr : ndarray of shape (>2,)
Increasing true positive rates such that element i is the true positive rate of predictions with score >= thresholds[i]. -
thresholds : ndarray of shape = (n_thresholds,)
Decreasing thresholds on the decision function used to compute fpr and tpr. thresholds[0] represents no instances being predicted and is arbitrarily set to max(y_score) + 1.



댓글남기기