AI 부트캠프 3주 : 선형대수

코드스테이츠와 함께하는 ‘AI 부프캠프’ 3주차

전반적 회고🎈

코드스테이츠 AI부트캠프 AIsection1 sprint3 과정에 참여하여 머신러닝을 위한 기초적인 공부(선형대수, 차원축소, 경사하강법)와 실습(PCA, 클러스터링)을 진행하였다.
고등학교수학과정이 나와서 당황했다. 손으로 계산하는 것은 어느정도 할 수 있겠는데, 코드로 구현하려니 많이 어색했다. 하지만 꾸준하게 라이브러리를 활용하여 계산하니 많이 익숙해져서 편한느낌, 내 것이 된 느낌이 들었다.
고등학교 수학과정에서 배웠던 내용들이 많이 나왔다. 그리고 직접 수학공식을 활용하니 점점 익숙해지고, 수학공식이 내것이 된 느낌이었다. 아는 것에서 만족하지 않고 익숙해져서 내것으로 만들어야겠다.
다양한 라이브러리들이 편리한 기능을 제공한다. 그 편리한 기능에 익숙해져야겠다. 어떤 라이브러리들이 있는지 살피고, 꾸준하게 실습하면서 익숙해지면, 비로소 그 기능들이 내것이 될 것이다.

학습내용📝

학습 기간

• Sprint 2기간 : 2022.12.23.(금) ~ 29.(목)

Linear Algebra

• python의 list와 numpy의 array의 차이
  • list : 수치적 연산이 불가능
  • array : 수치적 연산이 가능
• Scalar : 숫자
• Vector : 순서를 갖는 1차원 형태의 배열
  • 벡터의 크기 : 벡터의 길이, Norm, length, Magnitude
  • 벡터의 내적 : Dot Product, 곱하고더하고
  • 벡터의 직교 : 내적이 0
  • 단위 벡터 : Unit Vector, 길이가 1인 벡터
• Matrix : 행과 열
  • 행렬의 전치 : Transpose
    • $A^T$
    • $(A^T)^T=A$
    • np.transpose()
  • 행렬곱(Matrix Multiplication)
    • np.matmul()
  • 정사각 행렬(Square Matrix)
    • 행과 열이ㅡ 수가 동일한 메트릭스
  • 대각 행렬(Diagonal Matrix)
    • 주 대각선(principal diagonal)을 제외한 모든 성분이 0 인 정사각 행렬

      $D = \begin{bmatrix} a_{1,1} & 0 & 0
      0 & a_{2,2} & 0
      0 & 0 & a_{3,3} \end{bmatrix}$

  • 단위 행렬(Identity Matrix)
    • 대각 행렬 중에서 주 대각선 성분이 모두 1 인 매트릭스
    • np.identity() 또는 np.eye()
  • 역행렬(Inverse)
    • 임의의 정사각 행렬에 대하여 곱했을 때 단위 행렬이 되도록 하는 행렬
    • $A^{-1}$
    • np.linalg.inv()
  • 행렬식(Determinant)

    • 정사각 행렬 $A$에 대해서 det($A$) 또는 $

      A

      $로 표기

    • np.linalg.det()
    • 행렬식이 0 이면 역행렬이 존재하지 않음
• Span
  • 주어진 두 벡터의 조합으로 만들 수 있는 모든 가능한 벡터의 집합
  • 두 벡터가 선형 독립이면 2차원 span
  • 세 벡터가 선형 독립이면 3차원 span
  • 선형독립인 두 벡터(빨강, 초록)으로 만들 수 있는 벡터(파랑)들의 공간(연두)
    
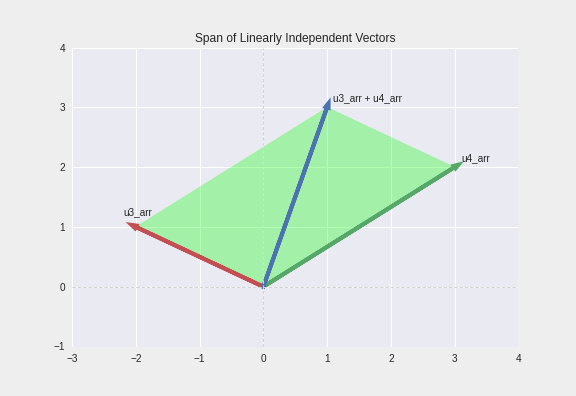
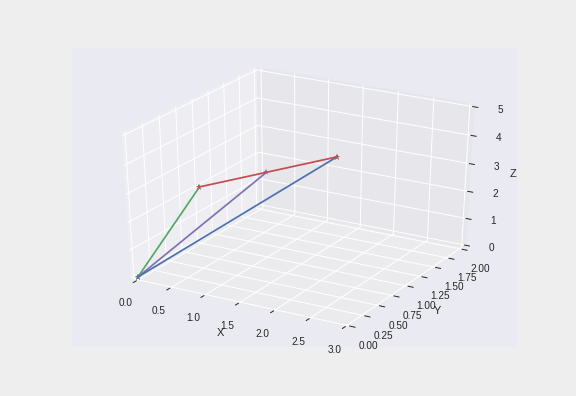
• Rank
  • 공간(span)의 차원
  • 아래는 3개의 행벡터로 이루어져 있지만 하나의 벡터(보라)가 다른 두 벡터(초록, 파랑)의 span에 종속되어 있어서 결과적으로 rank는 2, 곧 3개의 벡터가 2차원 공간을 이루는 모습
  • 빨강, 초록, 파랑의 평면 삼각형을 이룸
    

PCA

공분산과 상관계수

• 분산(Variance)
  • 데이터가 흩어져 있는 정도를 하나의 값으로 나타낸 것
  • 데이터가 서로 멀리 떨어져 있을수록 분산의 값이 커짐
  • 편차 제곱의 평균

  • $\sigma^2 = \frac{\sum{(X_{i} - \overline{X})^{2} } }{N} $ where $\ $ $X_i$:관측값 , $\bar{X}$:평균 , $N$: 관측값 개수

  • df.var() 또는 np.var()
  • 편차 = (관측값) - (평균)
  • 편차의 합은 항상 0 이기 때문에 편차의 평균도 항상 0
• 공분산(Covariance)
  • 공분산의 값이 크다면 두 변수 간의 연관성이 크다고 해석할 수 있다!
  • 하지만 분산은 데이터의 스케일에 영향을 많이 받기 때문에 값이 크다고해서 무조건 연관성이 크다고 할 수 없다.
  • 연관성이 적더라도 큰 스케일을 가지고 있다면 연관성이 높지만 작은 스케일을 가진 변수들에 비해서 높은 공분산 값을 가지게 된다.
• 분산-공분산 행렬(variance-covariance matrix)
  • 모든 변수에 대하여 분산과 공분산 값을 나타내는 정사각 행렬
    • 주 대각선 성분은 자기 자신의 분산 값
    • 주 대각선 이외의 성분은 가능한 두 변수의 공분산 값
  • df.cov() 또는 np.cov()
• 상관계수(Correlation coefficient)
  • 공분산을 두 변수의 표준편차로 나눠준 값

    $r_{x, y} = \frac{cov(X,Y)}{\sigma_{X}\sigma_{Y} }$

  • 공분산의 스케일을 조정하는 효과
  • 변수의 스케일에 영향을 받지 않음
  • -1에서 1 사이의 값을 가짐

  • 상관계수가 1이라는 것은 한 변수가 다른 변수에 대해서 완벽한 양의 선형 관계를 갖고 있다는 것을 의미

  • df.corr() 또는 np.corrcoef()

  • numpy를 사용하는 경우 df를 transpose 한 이유 [공식문서 numpy.corrcoef]
    • numpy.corrcoef(x, y=None, rowvar=True, bias=, ddof=, *, dtype=None)
      • Parameters
        • rowvarbool, optional
          • If rowvar is True (default), then each row represents a variable, with observations in the columns. Otherwise, the relationship is transposed: each column represents a variable, while the rows contain observations.
            • rowvar 파라미터는 기본값이 True로 되어있음
            • 곧, 각 행이 변수, 열이 관측값이라는 뜻
            • 반대(False)이면 전치(transpose) 됨

선형대수(Linear Algebra)

• Vector Transformation
  • 벡터의 변환은 벡터와 행렬 T 의 곱
  • np.matmul(메트릭스, 벡터)
• Eigenstuff
  • Eigenstuff는 np.linalg.eig()을 사용하여 구할 수 있음
  • np.linalg.eig() 으로 만들어진 eigenstuff는 2개의 배열을 갖음
  • 첫번째 배열은 Eigenvalue, 두번째 배열은 Eigenvector
  • Eigenvalue 의 인덱스, Eigenvector 의 column이 쌍을 이루는 eigenstuff 가 됨
  • eigenstuff 는 주어진 메트릭스의 column 갯수 만큼 생성 됨
• 고유벡터 Eigenvector
  • 주어진 transformation에 의해서 크기만 변하고 방향은 변하지 않는 벡터
  • 정방행렬 A에 대하여 Ax = λx (상수 λ) 가 성립하는 0이 아닌 벡터 x가 존재할 때 상수 λ 를 행렬 A의 고유값 (eigenvalue), x 를 이에 대응하는 고유벡터 (eigenvector) 라고 함
  • Eigenvector 는 크기가 1인 단위벡터
• 고유값 Eigenvalue
  • Eigenvector의 변화한 크기 값

주성분 분석(Principal Component Analysis, PCA)

• 주성분분석
  • 원래 데이터의 정보(분산)를 최대한 보존하는 새로운 축을 찾고, 그 축에 데이터를 사영(Linear Projection)하여 고차원의 데이터를 저차원으로 변환하는 기법
  • 주성분(PC)은 기존 데이터의 분산을 최대한 보존하도록 데이터를 projection 하는 축
  • PC의 단위벡터는 데이터의 공분산 행렬에 대한 eigenvector
  • eigenvector에 projection한 데이터의 분산이 eigenvalue
  • Feature Extraction 방식 중 하나
  • 기존 변수의 선형결합으로 새로운 변수(PC)를 생성
• PCA가 필요한 이유
  • 고차원의 문제(The Curse of Dimensionality; 차원의 저주)
    • sns.pairplot()
  • 비효율성, Overfitting(과적합)
  • 차원 축소(Dimensionality Reduction)
  • Feature selection
    • 데이터셋에서 덜 중요한 feature는 제거하는 방법
    • 분석 목적에 적합한 소수의 기존 feature를 선택
    • feature의 해석이 쉽다는 장점
    • feature 간 연관성을 직접 고려해야
  • Feature extraction
    • 기존 feature를 조합하여 사용
    • feature 간 상관관계를 고려하여 조합
    • 새로운 feature가 추출(생성)
    • 원래 변수들의 선형결합으로 이루어짐 ex) 집값 데이터셋에서 집 면적, 방 개수, 화장실 개수를 나타내는 변수를 조합하여 크기라는 하나의 변수를 사용
    • feature의 해석이 어려움
    • feature 수를 많이 줄일 수 있음

PCA 순서

• EDA
• 데이터 표준화
• 공분산 행렬 구하기
• Eigensruff 구하기
• Projection Data to Eigenvector

sklearn 을 활용한 PCA

Scree Plots

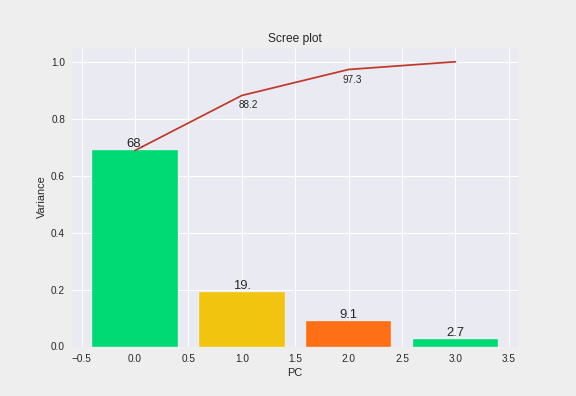
• scree plots을 활용해 주성분의 갯수 결정
  • 아래 그림에서 주성분이 두개가 되었을 때 누적분산이 88.2%가 되어 적절한 값으로 보임
  • 일반적으로 누적분산이 70~80% 이상이면 적절하다고 여겨짐

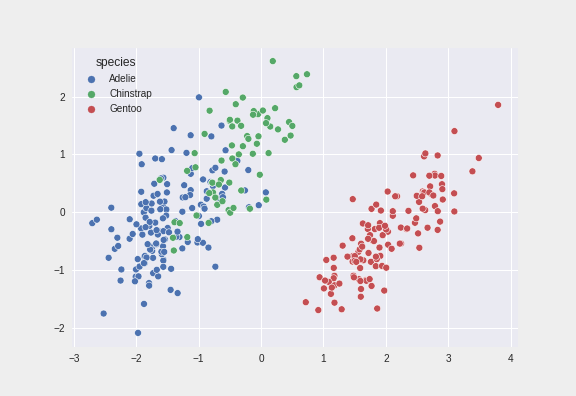
• 두 개의 주성분으로 만든 산점도
  • X축은 첫번째 주성분, Y축은 두번째 주성분

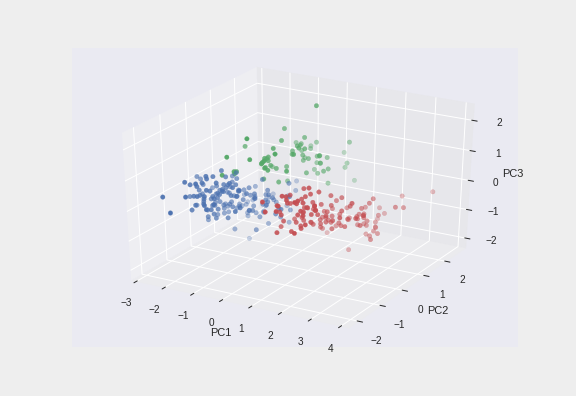
• 세 개의 주성분으로 만든 산점도
  • 첫 번째 주성분(PC1), 두 번째 주성분(PC2), 세 번째 주성분(PC3)
  • 세 번째 주성분은, 2D로 표현한 좌표평면의 산점도보다, chinstrap 펭귄의 위치를 더욱 입체적으로 구분할 수 있게 해준다.

Clustering

• 데이터 사이의 거리 계산하는 방법들
  • Euclidean Distance
  • Cosine Similarity
  • Jaccard Distance

• Hierarchical Clustering Dendrogram
  

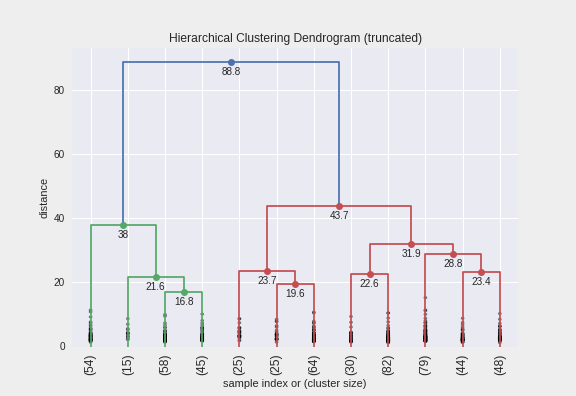
• 실제자료, K-Means Clustering, Hierarchical Clustering 비교
  

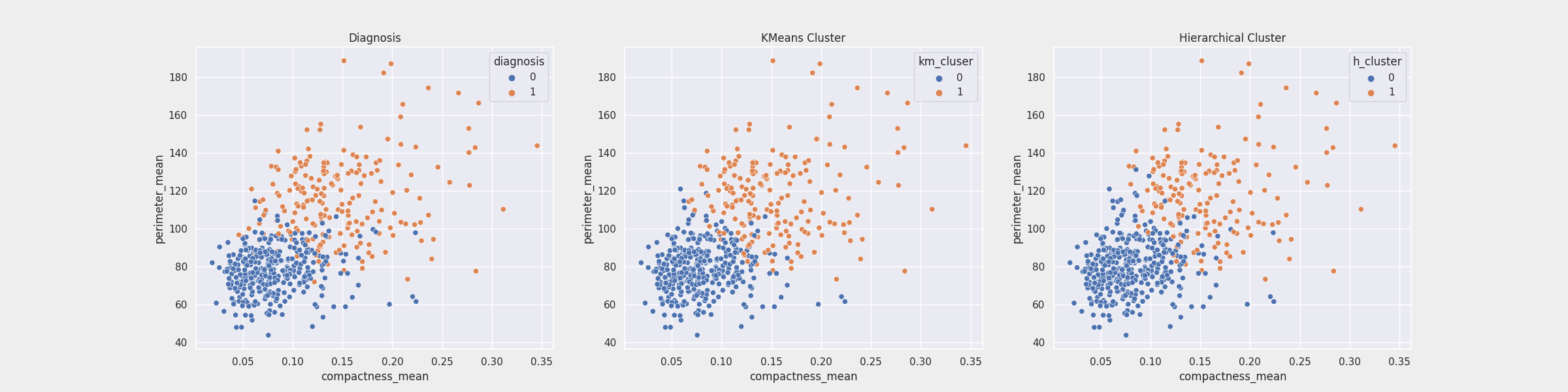
• diagnosis - K Means cluser 결합 비율 = 93.5%
• diagnosis - Hierarchical cluser 결합 비율 = 91.9%
• K-Means Clustering이 근소하게 결합률이 높음

미분, 경사하강법(Gradient Descent)

• 일반적인 미분 공식
  \(f'(x) = {f(x + \Delta x) - f(x) \over \Delta x}, \Delta x \rightarrow 0\)

• $\Delta x$는 0이 올 수 없기 때문에 0에 매우 근접한 값을 사용하게 됨
• 보통 $\Delta x$는 $1e-5$가 자주 사용됨
• 이렇게 $\Delta x$로 0에 근접한 수 $(1e-5)$를 사용하는 경우 이를 numerical method라고 표현함
• numerical method에서는 조금 더 정확한 측정을 위해 다음과 같이 계산 \(f'(x) = {f(x + \Delta x) - f(x - \Delta x) \over 2\Delta x}\)

미분공식

기본 미분공식

• $y = c$ (c는 상수) $ \rightarrow $ $ y’ = 0$
• $y = x^n$ (n은 자연수) $ \Rightarrow $ $ y’ = nx^{n-1}$
• $y = cf(x)$ (c는 상수) $ \Rightarrow $ $ y’ = cf’(x)$
• $y = f(x) \pm g(x)$ $ \Rightarrow$ $ y’ = f(x) \pm g(x)$ (복부호 동순)
• $y = f(x)g(x)$ $ \Rightarrow$ $ y’ = f’(x)g(x) + f(x)g’(x)$ (곱셈법칙)
• $y = f(x)g(x)h(x)$ $ \Rightarrow$ $ y’ = f’(x)g(x)h(x) + f(x)g’(x)h(x) + f(x)g(x)h’(x)$

• $y = f(g(x))$ $ \Rightarrow$ $ y’ = f’(x)g’(x)$ (연쇄법칙)

• 지수함수
  • $y = e^x $ $\Rightarrow$ $ y’ = e^x$
  • $y = a^x $ $\Rightarrow$ $ y’ = a^x \ln a$ $(단, a>0,\ a \neq 1)$
• 로그함수
  • $y = \log{x}$ $\Rightarrow$ $y’ = { {1} \over {x} } $

선형조합법칙

• $y = cf(x) + cg(x) ⇒ y’ = cf’(x) + cg’(x)$

곱셈법칙

• $y = f(x)g(x) ⇒ y’ = f(x)g’(x) + f’(x)g(x)$

• 예시 : $y = xe^x ⇒ y’ = xe^x + e^x$

연쇄법칙 chain rule

• $y = f(g(x))$ $ \Rightarrow$ $ y’ = f’(g)g’(x)$
• 예 : 정규분포의 확률밀도함수
  • $y = \exp { {(x - \mu)}^2 \over {\sigma}^2 }$
  • 위 함수는 다음과 같은 구조임
    • $y = f(g(h(x)))$
    • $f(g) = \exp(g)$
    • $g(h) = {h^2 \over {\sigma}^2}$
    • $h(x) = x - \mu$
  • 연쇄법칙을 적용하면 다음과 같음
    • $y’ = f’(g)\cdot g’(h)\cdot h’(x)$
    • $f’(g) = \exp(g) = \exp { {(x - \mu)}^2 \over {\sigma}^2 }$
    • $g’(h) = {2h \over {\sigma}^2} = {2(x - \mu) \over {\sigma}^2}$
    • $h’(x) = 1$
    • $y’ = \exp { {(x - \mu)}^2 \over {\sigma}^2}\cdot {2(x - \mu) \over {\sigma}^2}\cdot 1$
• 예 : 로그함수
  • $y = \log(x^2 - 3k)$
    • $y’ = {1 \over (x^2 - 3k)} \cdot 2x = {2x \over (x^2 - 3k)}$

2차 도함수

• 도함수를 한 번 더 미분하여 만들어진 함수를 2차 도함수(second derivative)라고 한다.

편미분

• 만약 함수가 둘 이상의 독립변수를 가지는 다변수 함수인 경우에도 미분 즉, 기울기는 하나의 변수에 대해서만 구할 수 있다. 이를 편미분(partial differentiation)이라고 한다.
• 편미분을 하는 방법은 변수가 하나인 함수의 미분과 같다. 다만 어떤 하나의 독립 변수에 대해 미분할 때는 다른 독립 변수를 상수로 생각하면 된다.

테일러 전개

• 함수의 기울기(1차 미분값)를 알고 있다면 함수의 모양을 다음처럼 근사화할 수 있다. x0는 함수값과 기울기를 구하는 x 위치이며 사용자가 마음대로 설정할 수 있다.
  • $f(x) \approx f(x_0) + {df(x_0) \over dx}(x - x_0)$
• 이를 테일러 전개(Taylor expansion)라고 한다. 다변수 함수의 경우에는 다음처럼 테일러 전개를 한다.
  • $f(x,y) \approx f(x_0,y_0) + {\partial df(x_0,y_0) \over \partial dx}(x - x_0) + {\partial df(x_0,y_0) \over \partial dx}(y - y_0)$

미분결과 시각화

• $f(x) = e^x$ 의 그래프

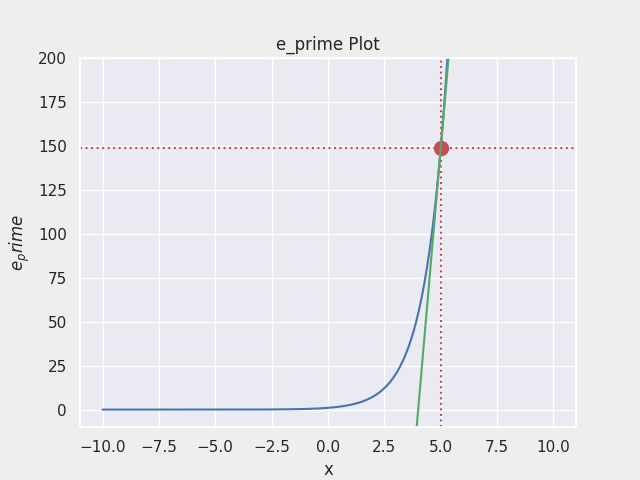
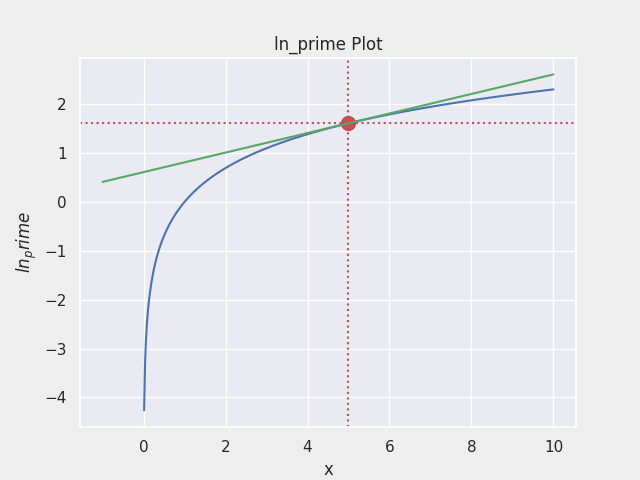
• $f(x) = lnx$ 의 그래프

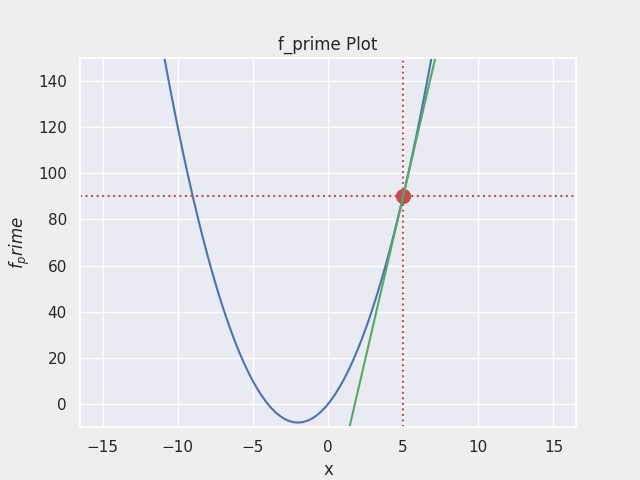
• $f(x) = 2x^2 + 8x$ 의 그래프

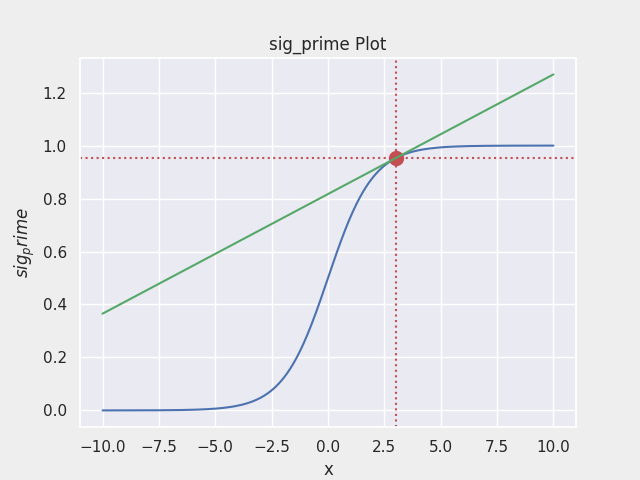
• $\sigma(x) = { {1} \over {1 + e^{-x} } }$ 의 그래프

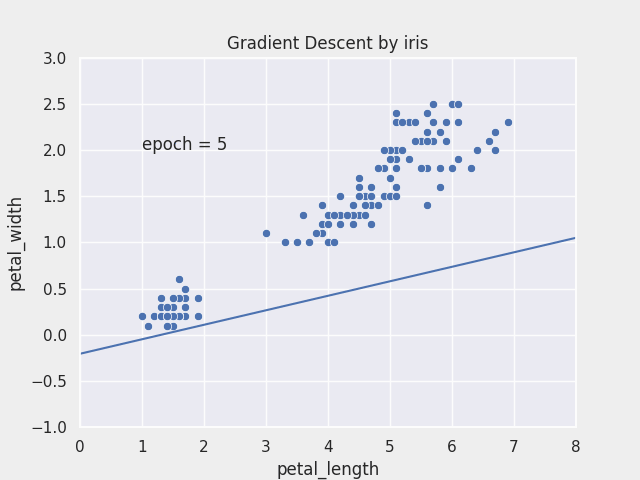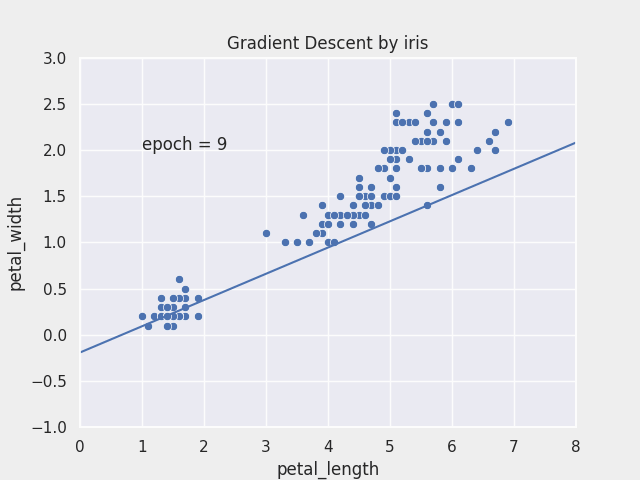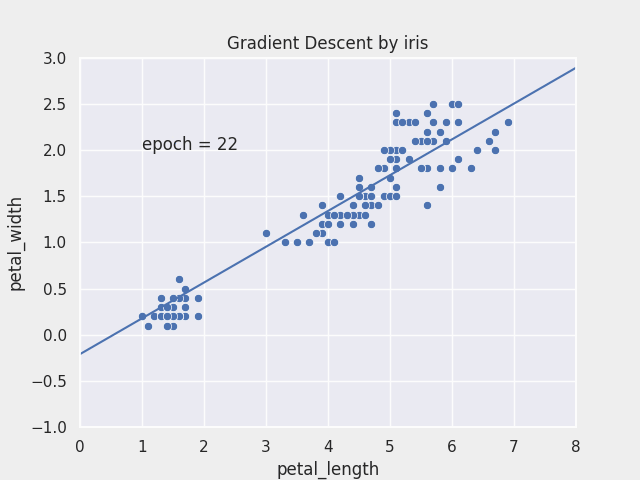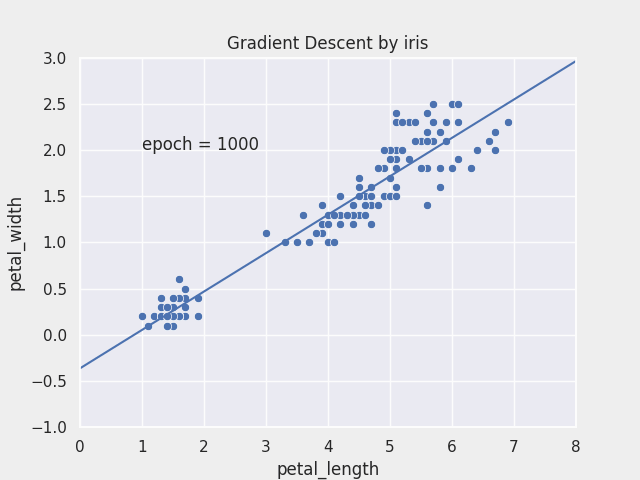
Gradient Descent

• 최적화 알고리즘의 대표
• 독립변수 $\theta_1$과 $\theta_2$을 변형시켜가며 오차 함수 $J(\theta_1, \theta_2)$ 의 최소값을 찾는 알고리즘
  • 오차 함수 $J(\theta_1, \theta_2)$ 의 최소값은 기울기가 0인 지점
  • 기울기가 양수라는 것은 $\theta$ 값이 커질 수록 함수 값이 커진다는 것을 의미하고, 반대로 기울기가 음수라면 $\theta$값이 커질수록 함수의 값이 작아진다는 것을 의미
• 오차함수
  • $Error Function = (ŷ^{(i)} - y^{(i)})^2$
    • $ŷ^{(i)}$ : i 번째 사례의 예측 값
    • $y^{(i)}$ : i 번째 사례의 라벨
• 비용함수
  • $MSE(θ,b) = {1 \over m}Σ(ŷ^{(i)} - y^{(i)})^2$
    $ = {1 \over m}Σ(θx^{(i)} + b - y^{(i)})^2$
    • $ŷ^{(i)}$ : i 번째 사례의 예측 값
    • $y^{(i)}$ : i 번째 사례의 라벨
    • $x^{(i)}$ : i 번째 입력 데이터 벡터
    • $θ$ : 가중치 벡터 (기울기)
    • $b$ : 편차 (y절편)
• 비용함수를 미분
  • $θ 편미분$
    • ${\partial \over \partial \theta}MSE(θ,b) = {1 \over m}Σ[(θx^{(i)} + b - y^{(i)})^2]’$
      $ = {2 \over m}Σ(θx^{(i)} + b - y^{(i)})[(θx^{(i)} + b - y^{(i)})]’$
      $ = {2 \over m}Σ(θx^{(i)} + b - y^{(i)})x^{(i)}$
  • $b 편미분$
    • ${\partial \over \partial b}MSE(θ,b) = {1 \over m}Σ[(θx^{(i)} + b - y^{(i)})^2]’$
      $ = {2 \over m}Σ(θx^{(i)} + b - y^{(i)})[(θx^{(i)} + b - y^{(i)})]’$
      $ = {2 \over m}Σ(θx^{(i)} + b - y^{(i)})$
• 경사하강 알고리즘 과정
  1. 경사하강법은 임의의 $\theta_1, \theta_2$를 랜덤으로 선택 즉, random initialization을 실행
  2. 반복적으로 파라미터 $\theta_1, \theta_2$를 업데이트 해가며, 오차 함수 $J(\theta_1,\theta_2)$ 값이 낮아지는 방향으로 진행
  3. 기울기가 커진다는 것은 오차함수 값이 커지는 방향이라는 것과 같기 때문에 경사하강법 알고리즘은 기울기의 반대 방향(기울기 $∇ J(\theta_1)$, $∇ J(\theta_2)$가 작아지는 방향)으로 이동
  4. 그리고 기울기가 0이 되어 global minimum에 도달할 때까지 이동
• 경사하강 알고리즘 수학적 공식 \(\theta_{n+1} = \theta_n - \eta ∇ J(\theta_n)\)
  • $\eta$는 학습률, $∇ J(\theta_n)$는 기울기를 의미
• 편미분 - 전미분의 차이
  • 편미분 : 하나의 변수를 고려한 하나의 접선의 기울기
  • 전미분 : 다양한 변수에 대해 다양한 접선의 기울기
    • 각각의 변수에 대한 편미분 뒤 모두 더하기 = 증분

끝까지 읽어주셔서 감사합니다😉