AI 부트캠프 19주
코드스테이츠와 함께하는 ‘AI 부트캠프’ 19주차
Section 5 : 컴퓨터 공학 기본 (Computer Science)
S5-Week 3 : Data Structure and Algorithm Intermediate
주간 회고
더 공부가 필요한 부분
- 알고리즘 문제를 접하면 어떻게 접근해야 하는지 모르겠다. 다양한 알고리즘 문제를 풀어보면서 문제를 유형화해야겠다.
5F 회고
-
사실(Fact)
해시테이블, 그래프 등의 자료구조를 배우고 DFS, BFS, DP 등 다양한 알고리즘을 배웠다. -
느낌(Feeling)
일단 머릿속으로 집어넣는 것 까지는 했는데, 몸으로 익숙해지지 않아서 자꾸 까먹는 것 같다. -
교훈(Finding)
기록하는 습관이 정말 중요한 것 같다. 처음 개발일지를 작성할 때는 해야한다고 하니깐 했는데, 잘 안까먹기 위하여, 잊어버려도 다시 빨리 찾기 위하여 기록은 반드시 필요한 것 같다. -
향후 행동(Future action)
다양한 자료구조와 알고리즘에 대하여 내 나름대로 정리하고 기록해야겠다. -
피드백(Feedback)
피드백을 해 주세요😀
N531 : Hash Table
Daily Reflection : 3L 회고
배운 것(Learned)
파이썬의 딕셔너리는 오픈어드레스방식의 해시테이블이다.
아쉬웠던 점(Lacked)
체이닝방식과 오픈어드레스방식의 차이가 어떠한 영향을미치는지 아직 모르겠다.
좋았던 점(Liked)
파이썬에 딕셔너리 자료구조가 있어서 참 다행이라는 생각이 들었다.
개요
🏆 학습 목표
- 기본적인 자료구조를 활용하여 다양한 프로그램을 위한 자료구조와 알고리즘에 대해서 익힌다.
- 중요한 자료구조인
Hash Table에 대해 배운다. 자료구조와알고리즘을 이해하며 프로그래밍하기문제해결과컴퓨팅 사고력기르기
키워드
- 해시테이블, 자료구조와 딕셔너리
학습
해시테이블
- 해시 테이블(hash table), 해시 맵(hash map), 해시 표는 컴퓨팅에서 키를 값에 매핑할 수 있는 구조인, 연관 배열 추가에 사용되는 자료 구조이다. 해시 테이블은 해시 함수를 사용하여 색인(index)을 버킷(bucket)이나 슬롯(slot)의 배열로 계산한다.[위키백과 : 해시테이블]
- 해싱의 장점
- 키를 통해 값을 검색하기 때문에, 데이터 양에 영향을 덜 받으며 성능이 빠르다.
-
파이썬의 딕셔너리는 내부적으로 해시테이블 구조로 구현되어있다.
- 해시함수
- 해시(Hash)를 반환해주는 함수
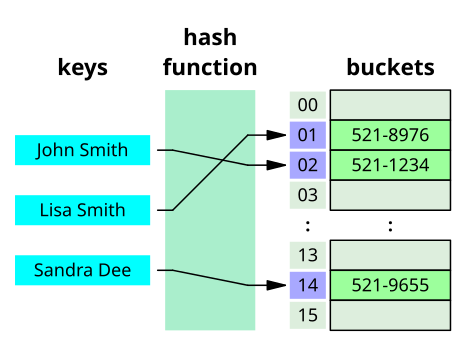
- 해시충돌을 최소화하도록 함수를 구성해야 함
- 해시(Hash)를 반환해주는 함수
- 해시함수에서 사용되는 메소드
hash(object): 공식문서print(hash('Lionel Messi')) # -6465434789167144040 print(hash('!@#$%^&*()-_=+[],./;')) # 3820050096850932095 print(hash(1988)) # 1988 print(hash(-256)) # -256str.encode(encoding='utf-8', errors='strict'): 공식문서encoded = 'Lionel Messi'.encode() print(encoded) print(len('Lionel Messi'), len(encoded)) for value in encoded: print(value, end=', ')📌 출력결과 b'Lionel Messi' 12 12 76, 105, 111, 110, 101, 108, 32, 77, 101, 115, 115, 105,encoded = '!@#$%^&*()-_=+[],./;'.encode() print(encoded) print(len('!@#$%^&*()-_=+[],./;'), len(encoded)) for value in encoded: print(value, end=', ')📌 출력결과 b'!@#$%^&*()-_=+[],./;' 20 20 33, 64, 35, 36, 37, 94, 38, 42, 40, 41, 45, 95, 61, 43, 91, 93, 44, 46, 47, 59,ord(c): 공식문서- 해당 문자의 유니코드 코드 포인트를 나타내는 정수를 반환
chr()는 반대로, 정수를 문자로 반환
print(ord('A')) # 65 print(ord('a')) # 97 print(ord(' ')) # 32 for t in 'Lionel Messi': print(ord(t), end=', ') # 76, 105, 111, 110, 101, 108, 32, 77, 101, 115, 115, 105,hashlib: 공식문서- 비밀번호와 같은 보안이 필요한 문자열을 유추나 복호화가 불가능한 형태로 저장하고 싶을 때, SHA256방식으로 해싱하는 방법
import hashlib m = hashlib.sha256() m.update(b"Nobody inspects") m.update(b" the spammish repetition") print(m.digest()) # 해싱한 바이트 문자열 반환 # b'\x03\x1e\xdd}Ae\x15\x93\xc5\xfe\\\x00o\xa5u+7\xfd\xdf\xf7\xbcN\x84:\xa6\xaf\x0c\x95\x0fK\x94\x06' print(m.hexdigest()) # 해싱한 16진수 문자열 반환 # 031edd7d41651593c5fe5c006fa5752b37fddff7bc4e843aa6af0c950f4b9406
해시충돌
- 해시충돌을 방지하는 방법
- 체이닝, 오픈어드레싱
- 체이닝 Chaining
- 해시가 중복되면 리스트로 연결하는 방법
- 리스트의 제한을 두지 않음
- 오픈어드레싱 open addressing
- 배열의 비어있는 인덱스를 찾아가는 방법
- 정해진 크기의 리스트를 사용
N532 : Graph
Daily Reflection : 3L 회고
배운 것(Learned)
그래프는 vert의 관계를 edge와 weight로 표현한 자료구조다.
아쉬웠던 점(Lacked)
아직 연습문제를 풀어보지 않아서 그래프에 대한 구체적인 이해가 부족한 것 같다.
좋았던 점(Liked)
트리와 그래프의 구분을 통하여 더욱 자료구조의 이해가 깊어진것 같다.
개요
🏆 학습 목표
그래프에 대한 기본개념을 배운다.순회를 배우고 그래프와 트리개념을 연관지어 이해한다.자료구조와알고리즘을 이해하며 프로그래밍하기문제해결과컴퓨팅 사고력기르기
키워드
- 그래프, 트리, 순회
학습
그래프
- 트리 자료구조와 비슷하지만
루프를 만들 수 있다는 특징이 있음 - Vert, Edge, Weight 등으로 이루어져 있음
- 인접행렬(Adjacency Matrix), 인접리스트(Adjacency List)로 구현
- Directed & Undirected : 방향성에는 양방향과 단방향이 있음
- 방향성(단방향)이 있는 그래프는 리프노드가 있을 수 있음
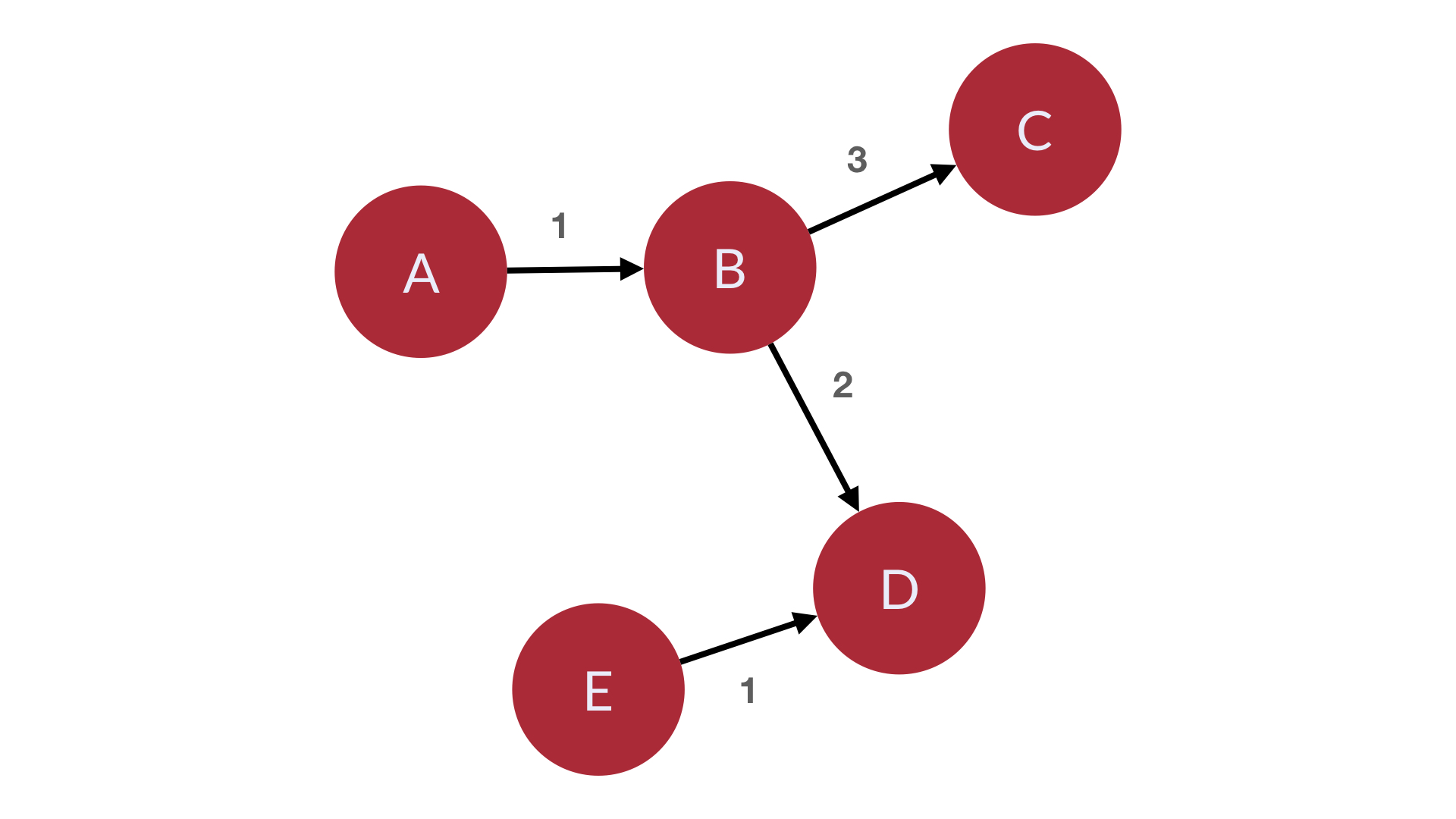
- 인접리스트
class Graph: def __init__(self): self.vertices = { "A": {"B": 1}, "B": {"C": 3, "D": 2}, "C": {}, "D": {}, "E": {"D": 1} }- 시간복잡도 : $O(n)$
- 공간복잡도 : $O(n+m)$
- 인접행렬
class Graph: def __init__(self): self.edges = [[0,1,0,0,0], [0,0,3,2,0], [0,0,0,0,0], [0,0,0,0,0], [0,0,0,1,0]]- 시간복잡도 : $O(n)$
- 공간복잡도 : $O(n^2)$
순회
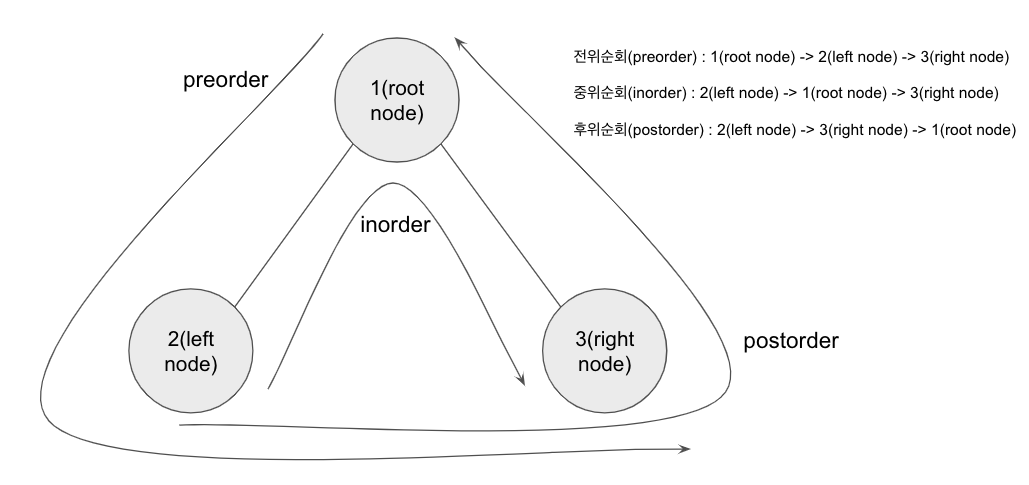
- 전위순회(Preorder Traverse) : 1-2-3
- 중위순회(Inorder Traverse) : 2-1-3
- 후위순회(Postorder Traverse) : 2-3-1
이진트리 순회 예시
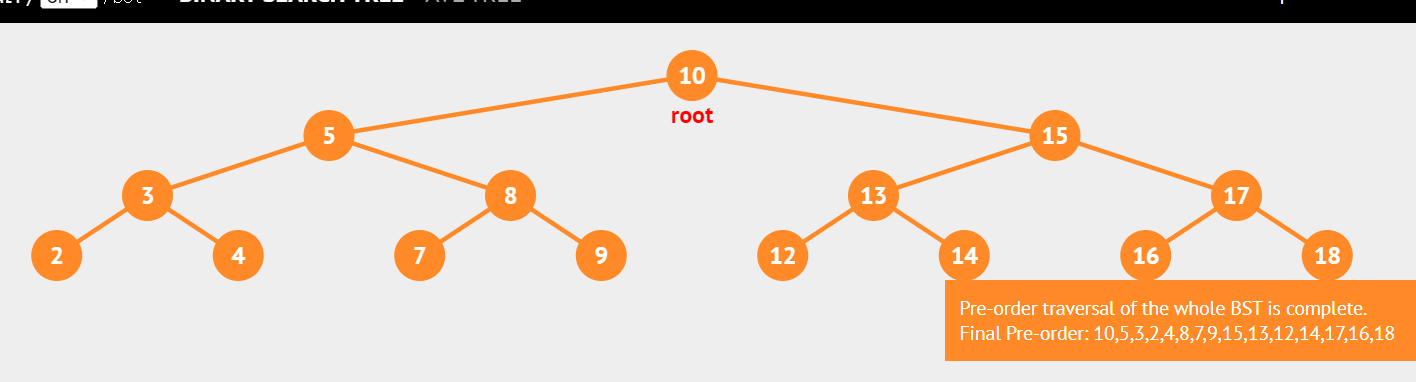
- 이진트리 만들기
# 이진 트리의 노드 클래스 class TreeNode: def __init__(self, val): self.value = val self.left = None self.right = None class binary_search_tree: def __init__(self, head): self.head = head def insert_node(self, value): self.base_node = self.head while True: if value < self.base_node.value: if self.base_node.left is not None: self.base_node = self.base_node.left else: self.base_node.left = TreeNode(value) break else: if self.base_node.right is not None: self.base_node = self.base_node.right else: self.base_node.right = TreeNode(value) break # 트리 입력 input_arr = [10,5,15,3,8,2,4,7,9,13,17,12,14,16,18] head = TreeNode(input_arr[0]) # 이진트리의 헤드 지정 bt = binary_search_tree(head) for i in range(1,len(input_arr)): # 이진트리에 배열 입력 bt.insert_node(input_arr[i]) - 순회 코드
# 전위 순회(pre-order) 함수 def preOrder(root): if root.value: print(root.value, end=' ') # 루트노드 if root.left: preOrder(root.left) # 왼쪽노드 if root.right: preOrder(root.right) # 오른쪽노드 # 중위 순회(in-order) 함수 def inOrder(root): if root.left: inOrder(root.left) # 왼쪽노드 if root.value: print(root.value, end=' ') # 루트노드 if root.right: inOrder(root.right) # 오른쪽노드 # 후위 순회(post-order) 함수 def postOrder(root): if root.left: postOrder(root.left) # 왼쪽노드 if root.right: postOrder(root.right) # 오른쪽노드 if root.value: print(root.value, end=' ') # 루트노드 # 순회 출력 테스트 print("전위 순회", end=' : ') preOrder(head) # 전위 순회 # 전위 순회 : 10 5 3 2 4 8 7 9 15 13 12 14 17 16 18 print("\n중위 순회", end=' : ') inOrder(head) # 중위 순회 # 중위 순회 : 2 3 4 5 7 8 9 10 12 13 14 15 16 17 18 print("\n후위 순회", end=' : ') postOrder(head) # 후위 순회 # 후위 순회 : 2 4 3 7 9 8 5 12 14 13 16 18 17 15 10
N533 : BFS와 DFS
Daily Reflection : 3L 회고
배운 것(Learned)
최단경로는 BFS, 공간효율성은 DFS
아쉬웠던 점(Lacked)
이해하는 것만도 벅차다! 학습리뷰를 끝내고 연습문제를 풀어봐야겠다.
좋았던 점(Liked)
동료코드보고 배울 수 있어서 좋았다.
개요
🏆 학습 목표
깊이 우선 탐색(depth-first search, DFS)을 배우고 DFS 코드를 이해한다.너비 우선 탐색(breadth-first search, BFS)을 배우고 BFS 코드를 이해한다.- 위의 개념과 기존에 배웠던 기본적인 스택, 재귀, 트리, 그래프 등을 연관지어 이해한다.
자료구조와알고리즘을 이해하며 프로그래밍하기- 문제해결과
컴퓨팅 사고력기르기
키워드
- BFS, DFS
학습
- 예시 그래프
graph = { 1: [2,3,4], 2: [5], 3: [6], 4: [], 5: [7], 6: [5], 7: [6] } import networkx as nx import matplotlib.pyplot as plt G = nx.DiGraph(directed=True) for node, edges in graph.items(): for edge in edges: G.add_edge(int(node), int(edge), weight=10) options = { 'node_size': 500, 'node_color' : [node for node in G.nodes()], 'cmap' : plt.get_cmap('cool'), } pos = nx.spring_layout(G, k=0.9) nx.draw_networkx(G, pos , arrows=True , **options) plt.show()
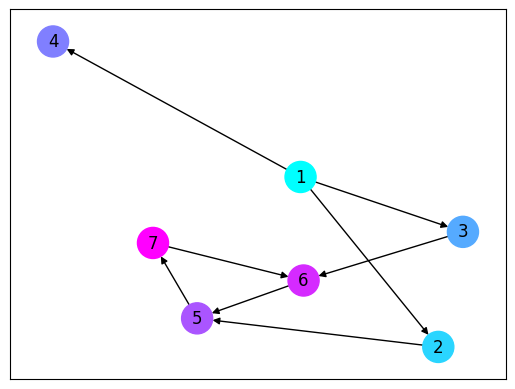
너비우선탐색 (BFS : Breadth-First Search)
- Queue를 이용하여 구현 : FIFO
- 깊이가 얕을 수록, DFS보다 효과적일 수 있음
- DFS보다 공간효율성이 낮을 수 있음
최단경로구하기에 활용- 활용 분야
- 길 찾기, 라우팅, BitTorrent와 같은 P2P 네트워크에서 인접 노드 찾기, 웹 크롤러, 소셜 네트워크에서 멀리 떨어진 사람 찾기, 그래프에서 주변 위치 찾기, 네트워크에서 방송, 그래프에서 주기 감지, 연결된 구성 요소 찾기
- BFS 코드구현1 : Queue
from collections import deque def bfs(start_node, graph, visited=[]): queue = deque([start_node]) while queue: cur_node = queue.popleft() if cur_node not in visited: visited.append(cur_node) queue.extend(graph[cur_node]) return visited print(bfs(1, graph, visited=[])) # [1, 2, 3, 4, 5, 6, 7]
깊이우선탐색 (DFS : Depth-First Search)
- Stack과 재귀방법을 활용하여 구현 : LIFO
- 깊이가 깊을 수록, BFS보다 노드를 찾는 속도가 빠름
- 해당 경로를 완벽하게 탐색하고자 할 때
- 활용 분야
- 가중 그래프의 최소 스패닝 트리 찾기, 길 찾기, 그래프에서 주기 감지, 미로 문제
- DFS 코드구현
# DFS : 재귀 def dfs_recur(start, graph, visited=[]): visited.append(start) for node in graph[start]: if node not in visited: dfs_recur(node, graph, visited) return visited print(dfs_recur(1, graph, visited=[])) # [1, 2, 5, 7, 6, 3, 4] # DFS : 스택 def dfs_stack(start_node, graph, visited=[]): stack = [start_node] while stack: node = stack.pop() if node not in visited: visited.append(node) stack.extend(graph[node][::-1]) return visited print(dfs_stack(1, graph, visited=[])) # [1, 2, 5, 7, 6, 3, 4]
N534 : Algorithm Advanced
Daily Reflection : 3L 회고
배운 것(Learned)
DP는 중복된 서브문제를 최소화하는 방법으로 메모이제이션과 태뷸레이션이 있다.
아쉬웠던 점(Lacked)
왜 메모이제이션이 하향식이고, 태뷸레이션이 상향식일까?
좋았던 점(Liked)
재귀의 부족한 부분을 DP로 해결할 수 있음을 배워서 좋다.
개요
🏆 학습 목표
- 알고리즘 개념을 숲을 보는 시점으로 생각하기.
Dynamic Programming(동적 계획법)에 대해 배운다.Greedy(그리디 - 탐욕 알고리즘)알고리즘에 대해 배운다.자료구조와알고리즘을 이해하며 프로그래밍하기- 문제해결과
컴퓨팅 사고력기르기
키워드
- Dynamic Programming, Greedy, Algorithm
학습
동적 계획법 (DP : Dynamic Programming)
- 문제의 일부분을 풀고 그 결과를
재활용하는 방법 - 동적 계획법(動的計劃法, dynamic programming)이란
복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 이것은 부분 문제반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱적은 시간내에 풀 때 사용한다. -
분할정복(Divide and Conquer)과 유사하지만 이미 계산한 결과를재활용하여 중복 계산을 최소화 한다는 차이가 있음 - 예 : 피보나치수열의
재귀 vs 동적계획연산 시간 비교# 재귀 방식 import time start_t = time.time() def fib(n): if n < 0: return '음수는 입력될 수 없습니다.' if n == 0: return 0 elif n == 1 or n == 2: return 1 else: return fib(n-1) + fib(n-2) n = 40 print(f'피보나치수열 {n}번째 수 : {fib(n):,}') print(f'소요시간 : {time.time() - start_t}') # 피보나치수열 40번째 수 : 102,334,155 # 소요시간 : 44.29799938201904# 동적 계획법 : 메모이제이션 import time start_t = time.time() calculated = {} def fib(n): if n == 0: return 0 if n == 1: return 1 elif n in calculated: return calculated[n] else: calculated[n] = fib(n-1) + fib(n-2) return calculated[n] n = 40 print(f'피보나치수열 {n}번째 수 : {fib(n):,}') print(f'소요시간 : {time.time() - start_t}') # 피보나치수열 40번째 수 : 102,334,155 # 소요시간 : 0.0009999275207519531# 동적 계획법 : 태뷸레이션 import time start_t = time.time() def fib(n): arr = [j for j in range(n+1)] if n < 2: return n for i in range(2, n+1): arr[i] = arr[i-1] + arr[i-2] return arr[n] n = 40 print(f'피보나치수열 {n}번째 수 : {fib(n):,}') print(f'소요시간 : {time.time() - start_t}') # 피보나치수열 40번째 수 : 102,334,155 # 소요시간 : 0.0010004043579101562
탐욕 알고리즘 (Greedy)
- 발견법(heuristic method)의 방법 중 하나
-
탐욕 알고리즘은 최적해를 구하는 데에 사용되는 근사적인 방법으로, 여러 경우 중 하나를 결정해야 할 때마다
그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도달한다. 순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적(전역적)인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다. 하지만 탐욕알고리즘을 적용할 수 있는 문제들은 지역적으로 최적이면서 전역적으로 최적인 문제들이다. - 탐욕알고리즘 예: 잔돈 갯수 구하기
def change_greedy(price, change_count = {}): change = 1000 - price coin_list = [500, 100, 50, 10] while change != 0: for coin in coin_list: change_bool = 0 change_bool = change_bool + (change // coin) change_count[coin] = change_bool change = change - (change_bool * coin) return change_count price = 220 print('잔돈 개수 :', change_greedy(price)) # 잔돈갯수 : {500: 1, 100: 2, 50: 1, 10: 3}



댓글남기기