AI 부트캠프 18주

코드스테이츠와 함께하는 ‘AI 부트캠프’ 18주차
Section 5 : 컴퓨터 공학 기본 (Computer Science)
S5-Week 2 : Data Structure and Algorithm Core
주간 회고
더 공부가 필요한 부분
- 알고리즘의 다양한 응용
5F 회고
-
사실(Fact)
파이썬의 자료구조와 알고리즘에 대하여 학습하였다. -
느낌(Feeling)
개념을 이해하고 코드를 따라할 수는 있지만 아직 낯설다. 그래서 아직 코딩테스트가 두렵고, 면접때 관련된 질문을 받으면 당황할 것 같다. -
교훈(Finding)
‘학습’, 學習 명사 1. 배워서 익히는 일. 익히는 과정이 아직 부족하다. -
향후 행동(Future action)
다양한 코딩테스트 문제를 풀어보면서 자료구조와 알고리즘에 대하여 익숙해지겠다. -
피드백(Feedback)
피드백을 해 주세요😀
N521 : DataStructure Fundamental
Daily Reflection : 3L 회고
배운 것(Learned)
큐 == fifo, 스택 == lifo
아쉬웠던 점(Lacked)
자료구조에 대한 이해가 부족한 상태에서 용어의 홍수에서 허우적대서 힘들었다.
좋았던 점(Liked)
머리는 많이 힘들었지만 가슴은 뿌듯하다.
개요
🏆 학습 목표
- 프로그램의 기반이 되는 자료구조와 알고리즘을 반복해서 학습
- 자료구조의 코어가 되는 추상자료형(ADT)과 함께 연결리스트, 큐, 스택의 설계에 대해 익힌다.
자료구조와알고리즘을 이해하며 프로그래밍하기- 문제해결과
컴퓨팅 사고력기르기
키워드
- 추상자료형, 파이썬 내장함수, Data Structure
학습
추상자료형(ADT : Abstract Data Type)
- ADT는 추상적으로 필요한 기능을 나열한 일종의 명세서(로직)
연결리스트(Linked List)
- 연결리스트는 참조(또는 포인트)로 구현
- 연결리스트는 길이를 별도로 지정해줄 필요가 없음
- 연결리스트의 각 요소는 참조하는 노드에 저장
- 여기서 노드는
컴퓨터의 메모리라고 이해하면 될 것 같음 - 여기서 참조는
연결(next)이라고 이해하면 될 것 같음
- 여기서 노드는
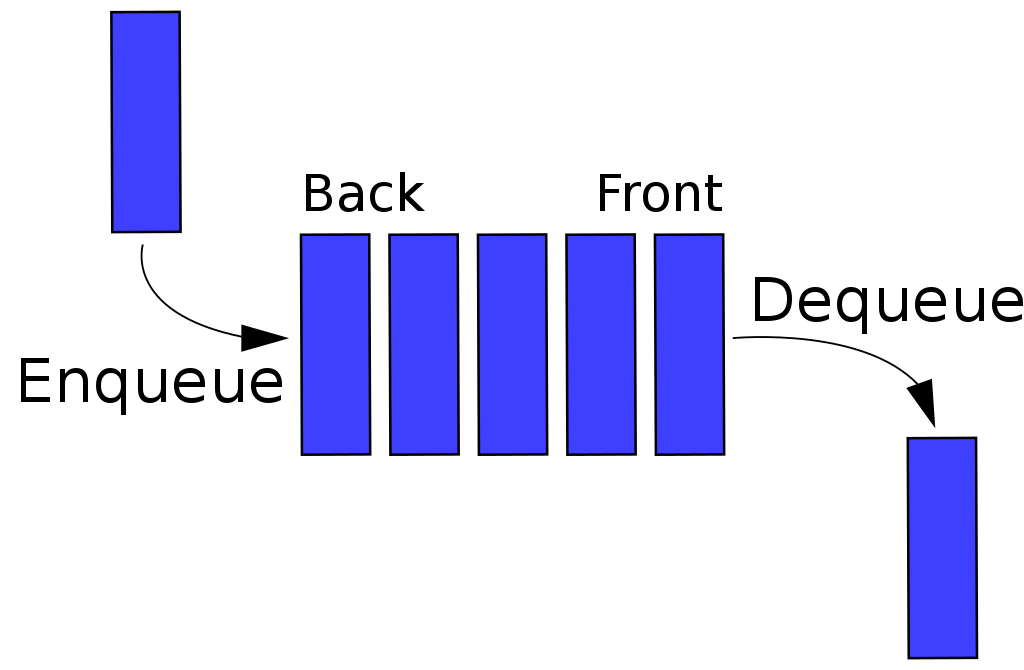
큐(Queue)
- 선입선출 , FIFO : First In First Out
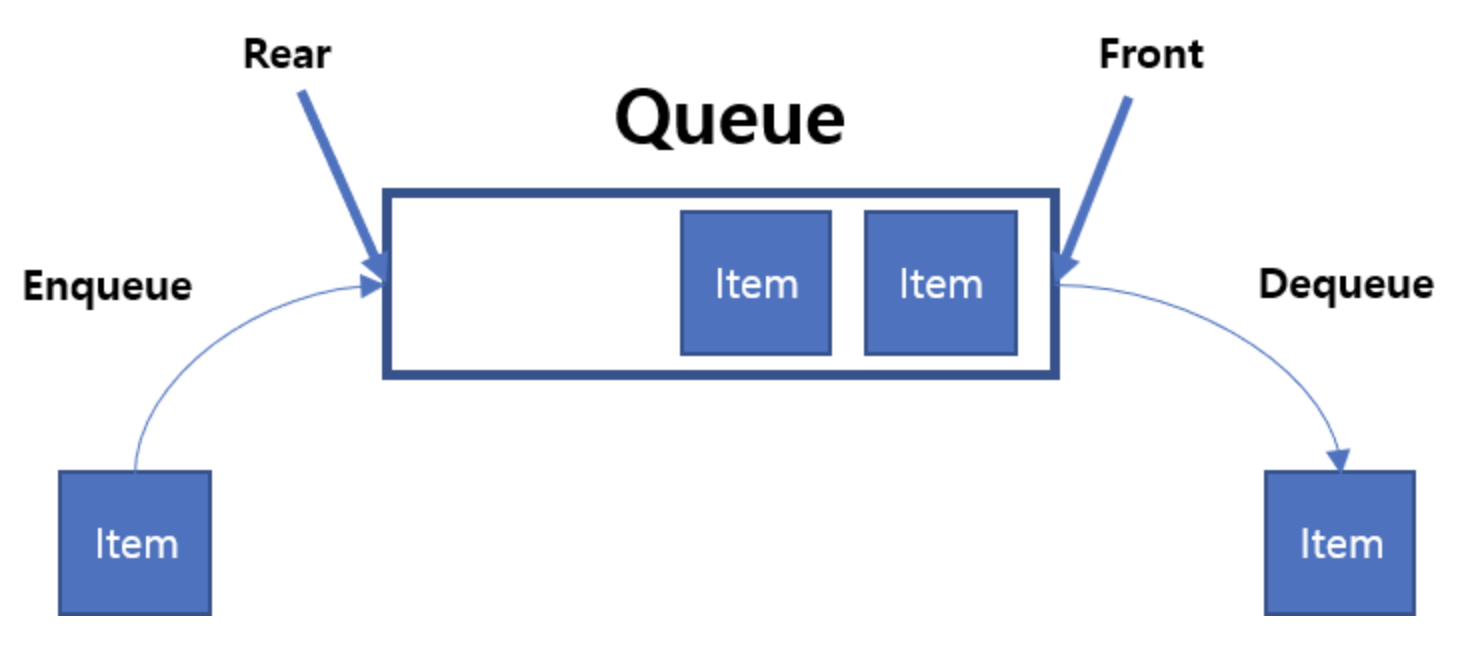
- enqueu : 넣기
- dequeue : 빼기
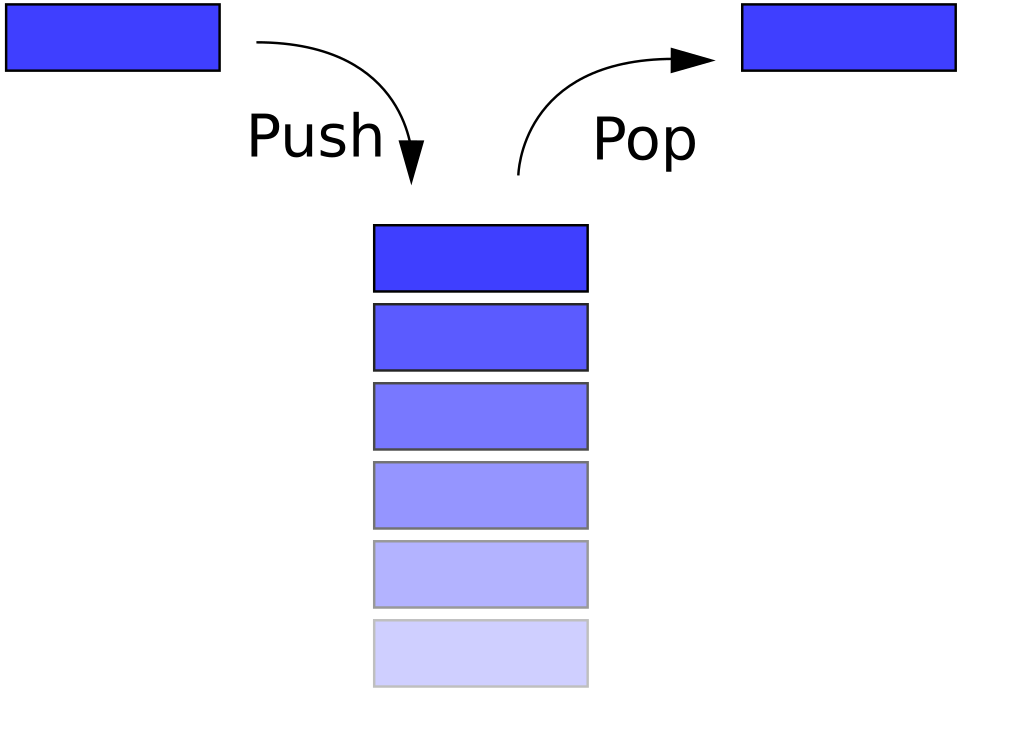
스택(Stack)
- 후입선출 , LIFO : Last In First Out
N512 : ataStructure Intermediate
Daily Reflection : 3L 회고
배운 것(Learned)
재귀는 자기자신을 호출한다.
아쉬웠던 점(Lacked)
자습자료는 아직 읽지 못했는데, 주말에 시간내서 공부해보고 싶다.
좋았던 점(Liked)
디버깅하면서 재귀함수의 동작을 확인하며 이해해서 좋았다.
개요
🏆 학습 목표
- 자료구조의 핵심개념인
검색과재귀에 대해 익힌다. 트리의 기본을 익힌다.알고리즘을 위한 논리적 방법자료구조와알고리즘을 이해하며 프로그래밍하기- 문제해결과
컴퓨팅 사고력기르기
키워드
- 검색과 재귀, 트리
학습
검색(Searching)
- 검색하는 컬렉션이 무작위이고 정렬되지 않은 경우, 선형검색이 기본적인 검색방법
- 반복문, 조건문을 이용한 선형 검색
def linear_search(arr, target): for idx in range(len(arr)): if arr[idx] == target: return idx return -1 print(linear_search([0, 1, 2], 2)) print(linear_search([0, 1, 2], 3))
재귀(Recursion)
- 재귀의 조건
- base case(기본 케이스 또는 조건)가 있어야 된다.
- 추가 조건과 기본 케이스의 차이를 확인한다.
- 반드시 자기 자신(함수)를 호출해야 한다.
-
단점 : 재귀를 사용하면 함수를 반복적으로 호출되는 상황이 벌어지므로, 메모리를 더 많이 사용
- 재귀의 예시 : 1. 일반 선형리스트 방법
# 일반 선형 리스트 my_list = [1,2,3,4,5] def sum_list(items): sum = 0 for i in items: sum = sum + i return sum sum_list(my_list) # 1+2+3+4+5 = 15 - 재귀의 예시 : 2. 위 문제를 하위 문제로 분리
1 + 2 + 3 + 4 + 5
(1 + (2 + 3 + 4 + 5))
(1 + (2 + (3 + 4 + 5)))
(1 + (2 + (3 + (4 + 5))))
(1 + (2 + (3 + (4 + (5))))) -
재귀의 예시 : 3. 재귀함수를 만들기 위한 의사코드를 작성
- 1단계 sum_list(items) if the length of items is 1 return the 1 item in the list - 2단계 sum_list(items) if the length of items is 1 return the 1 item in the list otherwise return the first item from the list + sum_list(the rest of the items) - 재귀의 예시 : 4. 실재 코드로 작성
def sum_list(items): print("items:", items) if len(items) == 1: # Base Case(항목이 1개인 경우가 기본 케이스) return items[0] # 재귀하지 않고 출력하고 끝남 else: return items[0] + sum_list(items[1:]) # items[:]는 한 항목씩 감소한다. print("sum_list:", sum_list([2, 3, 4, 5])) # 반복적으로 자기자신을 호출한다. - 재귀의 예시 : 5. 재귀함수 해석
sum_list()함수에[2, 3, 4, 5]입력되어, 출력은items[0] + sum_list(items[1:]), 곧,2 + sum_list([3, 4, 5])가 출력- “1”에서 출력 된
2 + sum_list([3, 4, 5])에서sum_list()함수가 다시 작동, 곧, 재귀하여sum_list([3, 4, 5])가3 + sum_list([4, 5])로 출력되어,2 + 3 + sum_list([4, 5])로 됨 - “2”에서 출력 된 것에서,
sum_list([4, 5])가 재귀하여4 + sum_list([5])로 출력되어,2 + 3 + 4 + sum_list([5])가 됨 - “3”에서 출력 된 것에서,
sum_list([5])는 길이가 1이기 때문에5만 출력되어, 최종 출력은2 + 3 + 4 + 5가 됨
재귀함수 예 : 피보나치수열
- 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열(위키백과)
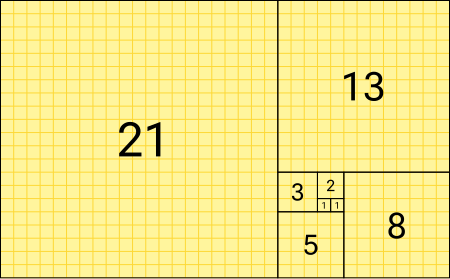
- 피보나치수열을 함수식으로 표현하면…
$f(1) = 1$
$f(2) = 1$
$f(3) = 2$
$f(4) = 3$
$f(5) = 5$
$f(6) = 8$
$f(7) = 13$
······
$f(n) = f(n-2) + f(n-1)$ - 의사코드
if n이 1 또는 2이면 1을 반환하고 끝 else f(n-2) + f(n-1)을 수행 - 코드실현
def fib(n): if n == 1 or n == 2: return 1 else: return fibo(n-2) + fibo(n-1) print(fibo(4)) # f(4) = 3 print(fibo(6)) # f(6) = 8 print(fibo(10)) # f(10) = 55 - 코드해석 : $f(4) = 3$
fib(4)는 n이 1또는 2가 아니기 때문에fib(2) + fib(3)을 반환fib(2)은 n이 2이기 때문에 1을 반환fib(3)은fib(1) + fib(2)를 반환fib(1)은 1을 반환fib(2)는 1을 반환
- 최종 1 + 1 + 1 = 3
-
참고
재귀함수 예 : 최대공약수(유클리드 호제법)
- 최대 공약수의 일반의미 : 두 수의 공약수 가운데 가장 큰 것
- 유클리드 호제법을 이용한 최대공약수
- 2개의 자연수(또는 정식) a, b에 대해서 a를 b로 나눈 나머지를 r이라 하면(단, a>b), a와 b의 최대공약수는 b와 r의 최대공약수와 같다
- $GCD(x, y) = GCD(y, x \% y)$, $(단, x > y)$
- 의사코드
x > y 일 때, if x % y == 0 이면 y를 최대공약수로 반환하고 끝 else 나머지 = x % y, 함수(y, 나머지) 재귀 - 실현코드
def gcd(x, y): if x < y : x, y = y, x # y가 x보다 더 크면 자리 바꿔 rem = x % y # x 나누기 y의 나머지 구하기 if rem == 0: # 나머지가 0이면 return y # y를 최대공약수로 반환하고 끝 else: # 아니면 return gcd(y, rem) # x자리에 y를 넣고, y자리에 나머지를 넣어서 재귀 print(gcd(1071, 1029)) # 21 print(gcd(78696, 19332)) # 36 - 참고
트리
- 트리 순회 방법
- 전위 순회(pre-order traverse): 루트를 먼저 방문합니다.
- 중위 순회(in-order traverse): 왼쪽 자신을 방문한 뒤에 루트를 방문합니다.
- 후위 순회(post-order traverse): 오른쪽 자식을 방문한 뒤에 루트를 방문합니다.
- 깊이(depth) : 트리에서 깊이(depth)는 각 노드의 루트노드로부터의 거리를 의미
-
차수(degree) : 각 노드에 연결되어있는 간선 개수
- 트리의 종류

N523 : Algorithm Fundamental
Daily Reflection : 3L 회고
배운 것(Learned)
선형검색의 시간복잡도는 O(n), 이진검색의 시간복잡도는 O(logn)
아쉬웠던 점(Lacked)
여러 알고리즘을 배웠는데, 구체적으로 어떻게 써야할지를 모르겠다.
좋았던 점(Liked)
알고리즘을 이해한 것으로 만족하자
개요
🏆 학습 목표
알고리즘 개념을 적용하여 프로그래밍하는데 익숙해지기- 알고리즘의
기본정렬에 대해 배운다. - OOP와 다른 프로그래밍 패러다임의 차이
자료구조와알고리즘을 이해하며 프로그래밍하기- 문제해결과
컴퓨팅 사고력기르기
키워드
교환개념, 정렬
학습
팩토리얼
- 재귀함수1
def factorial1(n): if n < 0: # 음수는 에러메시지 출력 return '음수는 입력될 수 없습니다.' elif n == 0 : # 0이면 1을 출력하고 끝 return 1 else : # n x 재귀 return n * factorial1(n - 1) print(factorial1(8)) # 40320 - 재귀함수2
factoral2 = lambda n : 1 if n == 1 else n * factoral2(n - 1) print(factoral2(8)) # 40320
이진검색
- 반복을 통해 숫자를 반으로 줄이면서 검색을 진행하기 때문에 선형보다 속도가 더 빠름
- 데이터가 이미 정렬된 경우에만 작동
- 선형검색과 이진검색 속도차이 비교
# 테스트 리스트 만들기 rand_int = list(range(0,100000000)) # 리스트 1억!! search_number = rand_int[-2] # 찾아야 하는 숫자는 하필 99,999,998 # 선형검색 @check_time def linear_search(linear_arr, search_number): for i in range(len(linear_arr)): if linear_arr[i] == search_number: return i print(f'Search index : {linear_search(rand_int, search_number)}') # ⌛ linear_search : 7.17179704 초 # 이진검색 @check_time def test_binary_search(binary_arr, search_number): low, high = 0, len(binary_arr) - 1 while low <= high: middle = (low + high) // 2 mid_value = binary_arr[middle] if mid_value < search_number: # 가운데 값이 찾는 값보다 작으면 low = middle # 가운데 인덱스를 최소인덱스로 변경 elif mid_value > search_number: # 가운데 값이 찾는 값보다 크면 high = middle # 가운데 인덱스를 최대인덱스로 변경 else: # 가운데 값이 찾는 값이면 return middle # 가운데 값을 반환하고 종료 return '인덱스를 찾지 못함' # 값을 찾지 못하는 경우 print(f'Search index : {test_binary_search(rand_int, search_number)}') # ⌛ test_binary_search : 0.00000000 초
Iterative Sorting(반복 정렬)
- Selection Sort(선택정렬)
- 가장 작은 노드(최소값)를 선택하고, 왼쪽부터 정렬을 하기 위해, 알맞은 위치와 교환하는 작업을 반복
- 서로 이웃하지 않은 노드를 교환하기 때문에 안정성이 떨어짐
- 최선, 최악 모두 $O(n^2)$
-
평균 : $O(n^2)$
- 소스코드
# 선택정렬 def selection_sort(li): length = len(li) for i in range(length-1): # 외부 반복문 : 처음부터 n-1까지 도는 반복문 min_index = i # 일단 i를 최소값이 있는 인덱스라 지정 for j in range(i+1, length): # 내부 반복문 : 최소값 인덱스를 찾는 반복문 if li[j] < li[min_index]: # 더작은게 나타나면 min_index = j # 최소인덱스를 j로 바꿔 li[min_index], li[i] = li[i], li[min_index] # swap return li # 테스트를 위한 랜덤 정수 리스트 만들기 import random import copy random.seed(83) rand_arr = [random.sample(range(1,101), 10) for _ in range(3)] # 범위, 요소개수, 리스트개수 rand_arr_back = copy.deepcopy(rand_arr) # 랜덤 정수 리스트 딥카피 sorted_arr = [selection_sort(arr) for arr in rand_arr] for i in range(len(rand_arr)): print(f'✅ Test {i+1}') print(f'{"Unsorted List":<15} : {rand_arr_back[i]}') # 랜덤 정수 리스트 print(f'{"Sorted List":<15} : {sorted_arr[i]}') # 정렬 된 리스트 print('='*60) - 출력결과
✅ Test 1 Unsorted List : [64, 59, 12, 17, 49, 5, 7, 84, 28, 25] Sorted List : [5, 7, 12, 17, 25, 28, 49, 59, 64, 84] ============================================================ ✅ Test 2 Unsorted List : [23, 40, 11, 7, 53, 20, 46, 39, 72, 26] Sorted List : [7, 11, 20, 23, 26, 39, 40, 46, 53, 72] ============================================================ ✅ Test 3 Unsorted List : [61, 81, 91, 30, 58, 22, 6, 4, 3, 97] Sorted List : [3, 4, 6, 22, 30, 58, 61, 81, 91, 97] ============================================================
- Insertion Sort(삽입정렬)
- 아직 정렬되지 않은 특정 노드와 정렬된 노드들의 값을 비교하고 값이 더 큰 것의 인덱스보다 작은 인덱스에 삽입하며 정렬
- 소량의 데이터 정렬에 효율적
- 최선(오름차순 → 오름차순) : $O(n)$
- 최악(오름차순 → 내림차순) : $O(n^2)$
-
평균 : $O(n^2)$
- 소스코드
# 삽입정렬 def insertion_sort(li): for end in range(1, len(li)): # 외부 반복문 for i in range(end, 0, -1): # 내부 반복문 if li[i - 1] > li[i]: # 앞이 뒤보다 크면... li[i - 1], li[i] = li[i], li[i - 1] # 둘의 자리를 바꿔라 return li # 테스트를 위한 랜덤 정수 리스트 만들기 import random import copy random.seed(83) rand_arr = [random.sample(range(1,101), 10) for _ in range(3)] # 범위, 요소개수, 리스트개수 rand_arr_back = copy.deepcopy(rand_arr) # 랜덤 정수 리스트 딥카피 sorted_arr = [insertion_sort(arr) for arr in rand_arr] for i in range(len(rand_arr)): print(f'✅ Test {i+1}') print(f'{"Unsorted List":<15} : {rand_arr_back[i]}') # 랜덤 정수 리스트 print(f'{"Sorted List":<15} : {sorted_arr[i]}') # 정렬 된 리스트 print('='*60) # 구분선 - 출력결과
✅ Test 1 Unsorted List : [64, 59, 12, 17, 49, 5, 7, 84, 28, 25] Sorted List : [5, 7, 12, 17, 25, 28, 49, 59, 64, 84] ============================================================ ✅ Test 2 Unsorted List : [23, 40, 11, 7, 53, 20, 46, 39, 72, 26] Sorted List : [7, 11, 20, 23, 26, 39, 40, 46, 53, 72] ============================================================ ✅ Test 3 Unsorted List : [61, 81, 91, 30, 58, 22, 6, 4, 3, 97] Sorted List : [3, 4, 6, 22, 30, 58, 61, 81, 91, 97] ============================================================
- Bubble Sort(버블정렬)
- 서로 이웃한 두 원소의 크기를 비교한 결과에 따라 교환을 반복
- 이웃노드만 교환하므로 안정적
- 최선(오름차순 → 오름차순) : $O(n)$
- 최악(오름차순 → 내림차순) : $O(n^2)$
-
평균 : $O(n^2)$
- 소스코드
# 버블정렬 def bubble_sort(li): length = len(li)-1 for i in range(length): # 외부 반복문 for j in range(length - i): # 내부 반복문 if li[j] > li[j+1]: # 앞이 뒤보다 크면... li[j+1], li[j] = li[j], li[j+1] # swap return li # 테스트를 위한 랜덤 정수 리스트 만들기 import random import copy random.seed(83) rand_arr = [random.sample(range(1,101), 10) for _ in range(3)] # 범위, 요소개수, 리스트개수 rand_arr_back = copy.deepcopy(rand_arr) # 랜덤 정수 리스트 딥카피 sorted_arr = [bubble_sort(arr) for arr in rand_arr] for i in range(len(rand_arr)): print(f'✅ Test {i+1}') print(f'{"Unsorted List":<15} : {rand_arr_back[i]}') # 랜덤 정수 리스트 print(f'{"Sorted List":<15} : {sorted_arr[i]}') # 정렬 된 리스트 print('='*60) # 구분선 - 출력결과
✅ Test 1 Unsorted List : [64, 59, 12, 17, 49, 5, 7, 84, 28, 25] Sorted List : [5, 7, 12, 17, 25, 28, 49, 59, 64, 84] ============================================================ ✅ Test 2 Unsorted List : [23, 40, 11, 7, 53, 20, 46, 39, 72, 26] Sorted List : [7, 11, 20, 23, 26, 39, 40, 46, 53, 72] ============================================================ ✅ Test 3 Unsorted List : [61, 81, 91, 30, 58, 22, 6, 4, 3, 97] Sorted List : [3, 4, 6, 22, 30, 58, 61, 81, 91, 97] ============================================================
정렬에 도움을 주는 메소드 itemgetter()
- 튜플로 구성된 리스트 정렬하기
from operator import itemgetter ex_arr = [('sera', 'A', 15), ('dave', 'B', 10), ('ann', 'C', 10)] sorted_1 = sorted(ex_arr, key=itemgetter(2)) print(sorted_1) # [('dave', 'B', 10), ('ann', 'C', 10), ('sera', 'A', 15)] sorted_2 = sorted(ex_arr, key=itemgetter(2,0)) print(sorted_2) # [('ann', 'C', 10), ('dave', 'B', 10), ('sera', 'A', 15)] - 딕셔너리로 구성된 리스트 정렬하기
from operator import itemgetter ex_dict = [ {'name':'sera', 'grade':'A', 'age':15}, {'name':'dave', 'grade':'B', 'age':10}, {'name':'ann', 'grade':'C', 'age':10} ] sorted_3 = sorted(ex_dict, key=itemgetter('age')) print(sorted_3) # [{'name': 'dave', 'grade': 'B', 'age': 10}, {'name': 'ann', 'grade': 'C', 'age': 10}, {'name': 'sera', 'grade': 'A', 'age': 15}] sorted_4 = sorted(ex_dict, key=itemgetter('age','name')) print(sorted_4) # [{'name': 'ann', 'grade': 'C', 'age': 10}, {'name': 'dave', 'grade': 'B', 'age': 10}, {'name': 'sera', 'grade': 'A', 'age': 15}] - 클래스로 구성된 리스트 정렬하기
from operator import attrgetter class Student: def __init__(self, name, grade, age): self.name = name self.grade = grade self.age = age children = [ Student('sera', 'A', 15), Student('dave', 'B', 10), Student('ann', 'C', 10), ] sorted_5 = sorted(children, key=attrgetter('age')) print([(x.name, x.grade, x.age) for x in sorted_5]) # [('dave', 'B', 10), ('ann', 'C', 10), ('sera', 'A', 15)] sorted_6 = sorted(children, key=attrgetter('age','name')) print([(x.name, x.grade, x.age) for x in sorted_6]) # [('ann', 'C', 10), ('dave', 'B', 10), ('sera', 'A', 15)] sorted_5를 SQL문으로 구현하기SELECT name, grade, age FROM Children ORDER BY 3;name grade age dave B 10 ann C 10 sera A 15 sorted_6를 SQL문으로 구현하기SELECT name, grade, age FROM Children ORDER BY 3, 1;name grade age ann C 10 dave B 10 sera A 15
N524 : Algorithm Intermediate
Daily Reflection : 3L 회고
배운 것(Learned)
분할정복의 예로 퀵정렬과 병합정렬이 있다.
아쉬웠던 점(Lacked)
퀵정렬이 생각보다 퀵하지 않다. 이걸 왜 퀵정렬이라고 하는건지 모르겠다.
좋았던 점(Liked)
파이썬의 특징을 살려 퀵정렬 코드를 간단하게 만들수 있어서 좋았다.
개요
🏆 학습 목표
- 프로그래밍과 코드분석에 익숙해지기
- 알고리즘을 활용한 프로그래밍
분할정복을 기반으로퀵정렬,병합정렬에 대해 배운다.알고리즘을 위한 논리적 방법자료구조와알고리즘을 이해하며 프로그래밍하기- 문제해결과
컴퓨팅 사고력기르기
키워드
분할정복과 재귀, 퀵정렬과 병합정렬
학습
분할정복(Divide and Conquer)
-
분할 정복 알고리즘(Divide and conquer algorithm)은 그대로 해결할 수 없는 문제를 작은 문제로 분할하여 문제를 해결하는 방법이나 알고리즘이다.[위키백과]
- 재귀의 예 : 1부터 n까지의 합
# 재귀: 1부터 n까지의 합 def func(n): if n < 1: # 1보다 작으면 0을 반환하고 끝 return 0 else: return n + func(n-1) # 더하고 n-1을 재귀 n = 10 print(f'1부터 {n}까지의 합 : {func(n)}') # 1부터 10까지의 합 : 55 - 분할정복의 예 : 1부터 n까지의 합
# 분할정복: 1부터 n까지의 합 def func(n): if n == 1: # n이 1이면 1을 반환하고 끝 return 1 elif n % 2 == 1: # n이 홀수이면... return func(n - 1) + n # n을 더하고 n-1을 재귀 else: # n이 짝수이면... n*(n+2)/4 (짝수합) return func(n / 2) * 2 + (n / 2) * (n / 2) n = 10 print(f'1부터 {n}까지의 합 : {func(n)}') # 1부터 10까지의 합 : 55.0
퀵정렬(Quick Sort)
- 시간복잡도
- 최악 : $O(n^2)$
- 피벗에 의한 원소들의 부분집합이 1개와 n-1개로 분할되는 경우가 반복되는 경우
- 이미 정렬되어있는 것을 또 정렬하는 경우
- 평균 : $O(nlogn)$
- 최악 : $O(n^2)$
- 불안전 정렬
- 퀵정렬의 장점
- 퀵 정렬은 피벗이라는 별도의 노드를 지정해두고 재귀적으로 수행을 하기 때문에 통상적으로 병합정렬보다 더 빠르다.
- 또한 한정적인 범위에서 데이터를 정렬하기 때문에 캐시를 덜 활용하고, 하드웨어적으로 효율적이다.
- 퀵정렬 : 코드1
def quick_sort(node, first, last): def partition(first, last): pivot = node[last] left = first for right in range(first, last): if node[right] < pivot: node[left], node[right] = node[right], node[left] left += 1 node[left], node[last] = node[last], node[left] return left if first < last: pivot = partition(first, last) quick_sort(node, first, pivot - 1) quick_sort(node, pivot + 1, last) # 테스트 test_arr = copy.deepcopy(rand_arr) print(f'{"Test Array Length":<18s} : {len(test_arr):,}') start_time = time.time() print(f'{"Usorted Array":<18s} : {test_arr[:5]}...') quick_sort(test_arr, 0, len(test_arr)-1) print(f'{"Sorted Array":<18s} : {test_arr[:5]}...') print(f'{"Running Time":<18s} : {time.time() - start_time}') # Test Array Length : 10,000 # Usorted Array : [1296, 5499, 1445, 7033, 435]... # Sorted Array : [0, 1, 2, 3, 4]... # Running Time : 0.03899860382080078 - 퀵정렬 : 코드2
def quick_sort(arr): if len(arr) <= 1: # 리스트의 길이가 하나 이하라면 반환하고 종료 return arr else: pivot = arr[0] # 첫번째 인덱스를 피봇으로 지정 left = [x for x in arr[1:] if x <= pivot] # 왼쪽 = 피봇보다 작거나 같은 것 right = [x for x in arr[1:] if x > pivot] # 오른쪽 = 피봇보다 큰 것 # 왼쪽리트스와 오른쪽리스트에서 재귀 반복 return quick_sort(left) + [pivot] + quick_sort(right) # 테스트 test_arr = copy.deepcopy(rand_arr) print(f'{"Test Array Length":<18s} : {len(test_arr):,}') start_time = time.time() print(f'{"Usorted Array":<18s} : {test_arr[:5]}...') test_arr = quick_sort(test_arr) print(f'{"Sorted Array":<18s} : {test_arr[:5]}...') print(f'{"Running Time":<18s} : {time.time() - start_time}') # Test Array Length : 10,000 # Usorted Array : [1296, 5499, 1445, 7033, 435]... # Sorted Array : [0, 1, 2, 3, 4]... # Running Time : 0.031996726989746094 - 퀵정렬 : 코드3
def quick_sort(array, start, end): if start >= end: # 원소길이가 1개 이하면 종료 return # pivot을 중심으로 left와 right를 나누는 과정 pivot = start left = start + 1 right = end while left <= right: # left와 right의 위치가 같거나 역전될 때까지 반복 # left는 왼쪽에서 오른쪽으로 이동하며 pivot보다 큰 데이터를 찾음 while left <= end and array[left] <= array[pivot]: left += 1 # right는 오른쪽에서 왼쪽으로 이동하며 pivot보다 작은 데이터를 찾음 while right > start and array[right] >= array[pivot]: right -= 1 if left > right: array[right], array[pivot] = array[pivot], array[right] else: array[left], array[right] = array[right], array[left] # 재귀 quick_sort(array, start, right-1) quick_sort(array, right+1, end) # 테스트 test_arr = copy.deepcopy(rand_arr) print(f'{"Test Array Length":<18s} : {len(test_arr):,}') start_time = time.time() print(f'{"Usorted Array":<18s} : {test_arr[:5]}...') quick_sort(test_arr, 0, len(test_arr)-1) print(f'{"Sorted Array":<18s} : {test_arr[:5]}...') print(f'{"Running Time":<18s} : {time.time() - start_time}') # Test Array Length : 10,000 # Usorted Array : [1296, 5499, 1445, 7033, 435]... # Sorted Array : [0, 1, 2, 3, 4]... # Running Time : 0.042000532150268555
병합정렬(Merge Sort)
- 시간복잡도
- 항상 : $O(nlogn)$
- 안정 정렬
- 동일한 값에 대해 기존의 순서가 유지
- 병합정렬 장점
- 병합 정렬은 전체 데이터를 기준으로 처음과 끝을 계속해서 탐색하기 때문에 퀵소트에 비해 느리다. 퀵 정렬보다 빠르지는 않지만, 안정(stable) 정렬이기 때문에 데이터가 중복되었더라도 영향을 덜 받기 때문이다.
- 퀵 정렬은 비교적 빠르지만 상황에 따라 편차가 크고, 피벗(노드) 설정 등의 다루기 어려운 점이 존재하기 때문에 실무에서는 활용되기가 어렵지만, 병합정렬은 상황에 상관없이 일정한 성능을 보이고, 퀵정렬에 비해 단순한 구조를 지닌다.
- 병합정렬 : 코드
def ms_divide(array): """ 병합정렬에서 주어진 배열을 분할하는 함수 """ length = len(array) if length == 1: # 배열의 길이가 1이 되면 재귀 종료 return array mid = length // 2 # 배열의 중간 # 재귀 gogo left = ms_divide(array[:mid]) right = ms_divide(array[mid:]) return ms_merge(left, right) def ms_merge(left, right): """ 입력된 두 배열을 오름차순으로 병합하는 함수 """ i, j, output = 0, 0, [] while i < len(left) and j < len(right): if left[i] < right[j]: # left가 작으면... output.append(left[i]) i += 1 else: # right가 작으면... output.append(right[j]) j += 1 output.extend(left[i:]) output.extend(right[j:]) return output # 테스트 test_arr = copy.deepcopy(rand_arr) print(f'{"Test Array Length":<18s} : {len(test_arr):,}') start_time = time.time() print(f'{"Usorted Array":<18s} : {test_arr[:5]}...') test_arr = ms_divide(test_arr) print(f'{"Sorted Array":<18s} : {test_arr[:5]}...') print(f'{"Running Time":<18s} : {time.time() - start_time}') # Test Array Length : 10,000 # Usorted Array : [1296, 5499, 1445, 7033, 435]... # Sorted Array : [0, 1, 2, 3, 4]... # Running Time : 0.06399893760681152
Link
- https://pythontutor.com/
- 디버깅 하듯이 코드를 한줄한줄 실행하며 각종 객체의 변화를 확인할 수 있음
- https://visualgo.net/en/bst
- 트리그래프, 정렬 등을 시각화하면서 코드의 실행과정을 그림으로 확인할 수 있음
- Quick Sort (퀵 정렬) python으로 구현하기
- 반복문으로 퀵 정렬 구현하기



댓글남기기